JF Ptak Science Books

Beautiful Techno-Art & Invention: Circular Adding Machines, 1850-1900

JF Ptak Science Books   Quick Post  

 

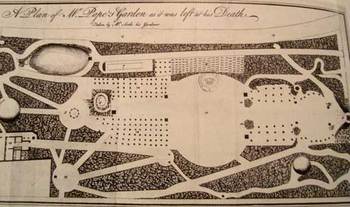
The Mathematical Garden--Alexander Pope and Found Geometries

JF Ptak Science Books (Revisiting an earlier post from 2008 with a added details).

While sitting at the edge of a stream in a flowing dress and shading herself with a yellow parasol, my wife and  the jewel in the crown, the brilliant Patti Digh, wrote a superb essay on following the paths less marked. (Maybe I'm making up the parasol bit. And the stream. And flowing dress.) I've always been a happy observer of found geometries, and her essay heightened my awareness to them, along with the conscious efforts that we may daily make to enforce these lines or follow a new, multi-dimensional geometric path. 

So when I stumbled across this map of Alexander Pope's garden and noticed the odd paths  winding their way through it, and  how much in contrast this was to the very sniffy upper  crust English garden of the 18th century, Patti's essay  lit instantly to mind—and also because in addition to being a geometer of emotion and thought she was in a past life a U VA English Master. 

Pope's garden was an irregular path in an irregular garden, that garden being his leased property at Twickenham, where he came to live in 1717, along with his mother and his boyhood nurse, Mary Beach, and his dog Bounce. 

Pope's garden was an irregular path in an irregular garden, that garden being his leased property at Twickenham, where he came to live in 1717, along with his mother and his boyhood nurse, Mary Beach, and his dog Bounce.  (Actually that would be a series of dogs as he named them all "Bounce".)  Pope was a poet and satirist and critic and general taste-maker-the social influence extending even to garden-making, as his was famous even during his lifetime, and not for the reasons that most English gardens were famous.

His was not the planned regularity of the gentility (and far of course  from the suffocating, critically flawed gardens at places like Versailles,  "Is there anything more shocking than the regularity of a planned  garden?" asks Batty Langley in his New Principles of the Gardening… 1728), and were removed from the "normal", more articulated garden.  I've never really understood the formal garden, especially as it relates  to the ancient analogies of gardens and paradise-the Garden of Eden, Pliny's Garden of Venus, Lucretius' Earthly Paradise, seem as though  they might be some sort of paradisical thing (though we won’t address  Bosch’s Garden of Earthly Delights) , but the formal gardens and its  paradise relationship seems odd, what with the removal of nature's "chaos" and all, unless that was indeed the Master Plan.

But the mathematical garden was a desirous thing—still is—and none  other than Christopher Wren wrote that it was “naturally more beautiful than any irregular figure” (1750).  There were some critics of the math garden, like Mr. Langley, but most garden  designers wrote and argued in favor of it, coming to the similar  conclusion of John Dennis, in that the Universe, being “regular in all its parts”  would dictate that its beauty be found as regular  in other things too,  “and it  is that exact regularity that [the mathematical garden] owes its admirable beauty” (1704). 
Pope didn't seem to address (in print) the garden idea formally except for a few places--  Pope praised 'the amiable simplicity of unadorned Nature' in a famous essay, published  in The Guardian in 1713, and then again in his message to Burlinton in 1731.

The plan of Pope’s garden was somewhat irregular, but to me the  most appealing aspect was  the irregularity of the paths that curled and snaked their way through the garden. 
And particularly,  what about the lower part  of the path along the bottom of J. Serle’s 1725 engraving?  What was that path in Pope's garden  leading to, or from?  Was there a particularly nice tree there, a  favorite spot, a cool shade, an odd bit of sunshine at sundown?  Or was this  wall-clinging path just the workman's route? 

Perhaps these weren’t Pope's principal desire lines in the garden—in fact, the garden desire lines  weren’t the garden at all— they might’ve been under it.  Pope’s famous grotto at Twickenham  may be better known than his garden-it certainly sounds  much more interesting. Followed his  own desire line, underground, in his famous grotto, which he began to build shortly after arriving at  Twickenham, and which was still under construction at the time of his death. 

The unseen desire lines of  Alexander Pope seem more fitting to me, more poetic, what with  Pope needing to dig out the earth in order to find what  he was looking for, rather than a more  simple wandering around his fine, rustic garden. 

Have a look at the materials house in the grotto/cabinet of curiosity here, along with a  commendable plan of the grotto itself.

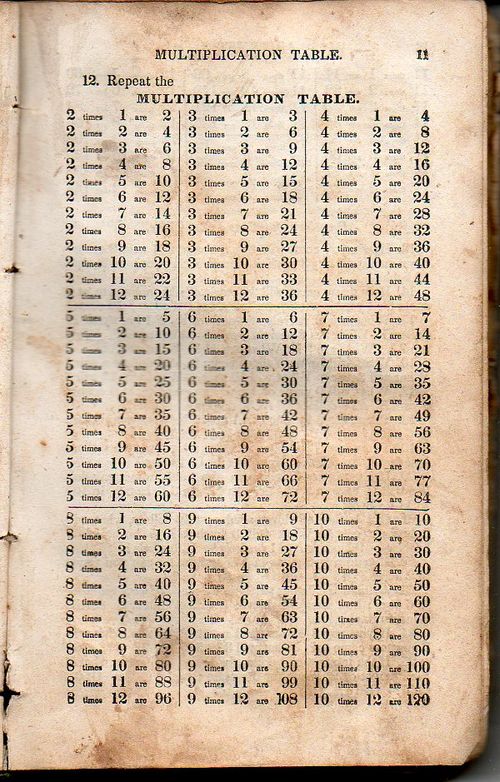
When Did "Are" Become "Is"? Beautful Mathematics, 1836

JF Ptak Science Books  Quick Post
 

This beautiful table appeared in Roswell W Smith's Practical and Mental Arithmetic, on a New Plan, in Which Mental Arithmetic is Combined with the Use of a Slate..., which was a soaringly successful book, this being the 53rd edition (!) and printed in Hartford in 1836.  (Smith was a busy man, writing several other standard and widely distributed works in geography and grammar).

But what we find here, in one of the many tables in the book, is the surprising "3 times 3 are 9" rather than what we normally hear in the U.S. as "3 times 3 is 9".  Perhaps what we are saying is "three threes are nine" or "seven threes are twenty-one", and so perhaps this really should be "are" rather than "is", except in the case of a number multiplied by one, when we would use "is" (as in "1x3 is 3", or "one three is three"). This would not be so for "3x1" where we are saying "three ones are three"). 

We can also disregard both of those words and simply say "equal". Or is that "equals"?

Its a small thing, I know, and I was attracted to the beauty and simplicity and assurance of the table--it is simply a finely designed thing.

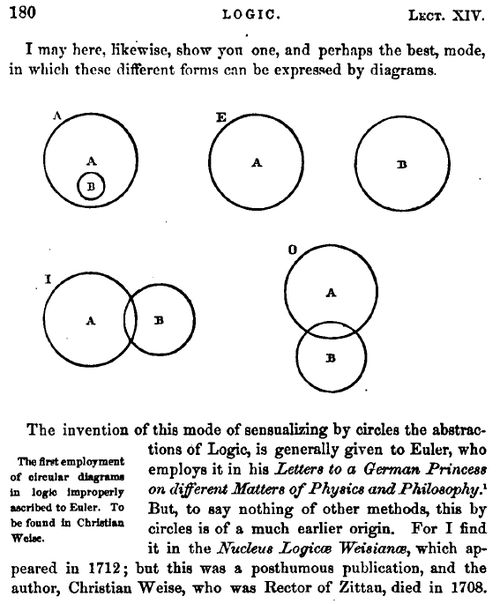
A Note on Venn and his Diagrams

JF Ptak Science Books   Post 1952
 

It seems so unlikely that the Venn diagrams took so long to appear, that it hadn't been Aristotle's Diagrams, or Cartesian Diagrams; rather, these elegant creations--about a different way to represent propositions by diagrams-- belong to Mr. Venn's invention in 1880. Mostly. It was in that year that these famous more fully-developed diagrams first appeared in a paper entitled "On the Diagrammatic and Mechanical Representation of Propositions and Reasonings" in the Philosophical Magazine and Journal of Science.  They seem so beautiful, and so simple, and so powerful, and so elegant. So necessary.  And so why-did-they-take-so-long-to-appear, so obvious.  In a way, they are in that category of The Great Obvious Invention, in a similar vein to Mr. Luke Howard first classifying the names of clouds  in 1803.  Sometimes things are not obvious until they are.  

 

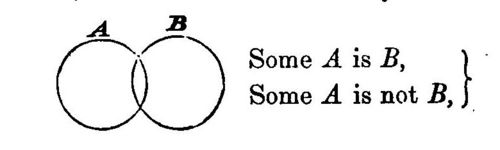
[Source: Internet Archives, John Venn, Symbolic Logic, 1881, full text.]

Well, almost.  The diagrams did mostly make an appearance earlier--though not in the Venn form--in the work of Christian Weise (d. 1708) and then in that of Leonhard Euler (1707-1783), that according to the great William Rowan Hamilton, explained in his work Metaphysics and Logic (1858-1860). But the final form seems to be that of Venn.  

Hamilton's work appears so:

 

They also appeared in the Proceedings of the Cambridge Philosophical Society, volume 4, 1880, in his article "On the employment of geometrical diagrams for the sensible representation of logical propositions" (here) in which he discusses the history of the diagrams, including the Hamiton history.  Venn also includes this beautiful logic template of Bolzano:

I found a wonderful book review of Venn's book Symbolic Logic that appeared the following year, appearing in the journal Nature on 14 July 1881, and reviewed by the inimitable W. Stanley Jevons (which is reproduced below).

Index: Computer Chronology, 50-Year Micro List, 1938-1988

This is a simple and basic outline for a chronological list of computers constructed from 1938 (with the Konrad Zuse "Z1" in Germany) through the Alliant series in 1988. 

Key:  listings are by Maker/Name of the computer/Country of origin/Year

Example:   Zuse     Z1     Germany     1938  (So, the ZI computer made in 1938 by Konrad Zuse, in Germany)

Here's a terrific piece of work called  "The Computer Tree", from Electronic Computers Within the Ordnance Corps , by Karl Kempf. "U.S. Army Diagram", the source of this information coming from the U.S. Army, here.

This image is expandable.

I've found a supplement for computer tree above. .  The new one is interesting and has its differences from its predecessor, and divides its generations of computers in terms of logic technology. It is found in a 1960 NSF pamphlet called "The Family Tree of Computer Design", a Brief Summary of Computer Development, and I found its reference in a good book by I.B. Cohen, Howard Aiken, Portrait of a Computer Pioneer, published by MIT and available here. 

[Image source: Microsoft.]

 

 

Feeling and Touching Calculated Numbers in the 18th Century: Palpable Mathematical Devices

JF Ptak Science Books  Revisting/Expanding Post #76 (from 2008)

Part I:

Nicholas Saunderson (1682-1739)  was an extraordinary mathematical talent—he was also blind (from about the age of one), and invented, principally for his own uses, what I think is the first mathematical calculator designed specifically for the use of the blind.

He was supremely gifted and creative, and rose to become the fourth Lucasian professor at Cambridge, succeeding the expelled William Whiston, who had in turn succeeded Isaac Newton—Saunderson also held the post for one of the longest periods of time, 1711-1739.  He was friend and associate to Newton, Whiston, Roger Cotes, Halley, De Moivre and others during a particularly rich intellectual period in the history of physics and the maths. 


His calculator was smart and simple, based on a cribbage-board –like device, that was able to perform arithmetical and algebraic functions—it consisted of nine rows and was worked with two pins, the positioning of the pins on the engraved board telling the user their value. (There was another calculator for the blind constructed by Meyer (below, left)  using a sort of reverse principle to the Saunderson model where it was the shape and placement (leaning or not, for example) of the pegs in the hole that annotated value rather than their placement on the board.

The Saunderson computer was described in his The Elements of Algebra…, published at Cambridge in the first edition just after the author’s death, in 1740.  The device was described in the book by John Colson (who succeeded Saunderson to the Lucasian chair), who commented that it was via the use of the device that
Saunderson could compose his treatise on algebra. (Above  is another Saunderson-based calculator allowing for the construction and study of geometrical figures).  

Part II:

"Palpable Arithmetic", the sub-heading for the sheet illustrating aspects of algebra for Abraham Rees' (1743-1825) great if not problematic 45-volume Cyclopedia, is a system that  records and organizes and sometimes calculates using three dimensional objects.

For example the Egyptians (for one) calculated with pebbles; then there was the ABAX of the Greeks, and the abacus (and also called the mensa Pythagoras) of the Romans (and of the Japanese and earlier still of the Chinese), the scaccarium of the English (via the Norman conquest), and innumerable other systems that performed arithmetic and recording and
archiving functions via the employment of reeds, notches on a tree or cloth or stick (etc.), reeds, knots, fingers, beans,shells, string, sand, and on and on.  Palpable arithmetic also has a specialized meaning in places as a calculating device in which the numbers are recognized by touch and used by blind mathematicians or other parishioners. (Just for the record, there are a number of eminent blind  mathematicians including, for example,  Leonard Euler (1707–1783, who was blind in the last 17 years of his life), Nicholas Saunderson (who I wrote about in an earlier post), Louis Antoine (1888-1971), Lev Pontryagin (1908-1988.)) 

An interesting and very large philosophical issue that comes up here with the blind mathemaitican is the concept of image formation and its dependence upon sight for intuition, as with geometry or topology.    Plato for one determined for himself that image formation issues were precognate and the same in sight and non sighted people.  How would you manipulate a geometrical form if you’ve never actually seen one, or how would you extend you spatial imagination of compex forms without a reference? 

But my main issue here is the image from the hees book.  I'm by the meaning of this particular calculator or recording system--I just can't tell what it is.  Can you?  If so I'd love to hear from you.

Note on the Anthropology of Numbers:

From Levi Leonard Conant's The Number Concept Its Origin and Development we find these very descriptive definitions of words for numbers, all of which relate to the sort of implement that they were controlling
their numbers with, or calculating:

"in Javanese, Malay, and Manadu, the words for 1, which are respectively
siji, satu, and sabuah, signify 1 seed, 1 pebble, and 1 fruit
respectively. Words as natural and as much to be expected at the
beginning of a number scale as any finger name could possibly be. Among
almost all...the derivation of number words from these sources can constitute no ground
for surprise. The Marquesan word for 4 is pona, knot, from the practice
of tying breadfruit in knots of 4. The Maori 10 is tekau, bunch, or
parcel, from the counting of yams and fish by parcels of 10. The
Javanese call 25, lawe, a thread, or string; 50, ekat, a skein of
thread; 400, samas, a bit of gold; 800, domas, 2 bits of gold.The
Macassar and Butong term for 100 is bilangan, 1 tale or reckoning..."

The full sheet from the Rees book:

Opening the Doors to Trigonometric Heaven

JF Ptak Science Books   Quick Post  

There aren't many other title pages in the history of mathematics that swing the doors of beauty and heaven and opportunity and logic and thought than the (appropriately-named) Bonaventura Francesco Cavalieri/Cavalerius.  A Milanese (1598-1647) who taught at Pisa and who published eleven books and worked in wide fields in mathematics as well as astronomy and physics, published his Trigonometria... in Bologna in 1643, and sent a fabulous image to his new readers right there on his very illustrated and augmented title page. 

Seldom have the doors of knwoledge been thrown open so wide and invitingly as this, with Trigonometria lightly awarding the reader with a new portal to fantastic opportunities--who wouldn't want to walk on in?  The tools of trig are displayed on the ground at Trionometria's feet (arranged and not by happenstance), while five figures employ these same tools in the background hills, which are being bathed in a pure holy light of some sort, an inspiration from the sky.  The doors are decorated with astronomical figures and light calculation, as well as polyons and geometrical drawings.  And just to make sure that the author meant what he intended, we can see above the full/thick wind-blown hair of Trigonometria (which in itself seems very unusual to me, such a carefree adn tossled attitude) a fruit-garland, a horn of plenty in its way.  Make no mistake--Cavalieri was making a king-sized offer to his reader to open their brains. 

I did leave out a major part of the title--the section dealing with logarithms, which is basically a reprint of Cavalieri's early work (done in 1632), and which was the first work in Italian on that subject. 

 

Vernacular Found-Polygonism 2: Walker Evans on the Roof

JF Ptak Science Books  Quick Post

How many polygons can you find? 

"Walker Evans climbed to the roof of the Fisk Building on Central Park South to  photograph the web of steel struts and electric signs that were rapidly filling the skies over Manhattan. The electric signs in this photograph alternately  flashed the company's name and the names of its two principal products. As there  were approximately a hundred million wheels rolling over America's roads in  1928, the sale of tires quickly overtook that of rubber galoshes. The image  expresses Evans' conviction that modern art could be timeless yet topical when  perfectly wrought of vernacular materials."--Metropolitan Museum of Art

This is one in a series of posts made on found geometries--here are a few others:

Found Alphabets and Geometry in Stone.(here)

Magritte-Like Disorienting Geometry in Found-Art Urban Design, 1925 (here)

Sierpinski Triangles & the Empire State Building (here)

 

A Few Examples of Renaissance Icons in Science Emblemata

JF Ptak Science Books   Post 1885

These images come from a later (and English edition) of Cesare Ripa's essential keybook to Renaissance iconogrpahy, the Iconologica overa descittione d'imagini delle virtu, viti, affetti, passioni humane...first published in the early 1590's with Ripa's artwork.  I don't much like the English version of his work, nor do I care that much for the artwork (inferior in most ways to the great craftsman-like feel of the Renaissance images), though it does serve the purpose of place-holding the symbolism and explaining the elements of the icons.

I've chosen a few emblems for the sciences to illustrate this important work of deduction and explanation, as it would be an aid to anyone interested in the art of the Renaissance--and that would be an interest at virtually any level.

I chose "Arithmetic" as my first example because of the lovely parallels found in the folds of Arithmetic's dress--musical notation, underneath which we see the faint "Pars Impars" (even and odd) to help settle the old scores of symmetry.  The connection between music and mathematics is thousnads of years old, and though I might've used "mathematics" rather than its oldest branch (of "arithmetic") to show the ancinet connection between music and numbers, it should be remembered that not every aspect of arithmeic is standard, and that there is a good and strong relation between music and "higher arithmetic" (number theory).  In general I just like the emblzoned connection here between the two, showing a temporal sequencing representation, a placing of music in relation to number right out there in time-and-space,an adept of the mental image of music. There is no doubt that when a viewer was finsihed with this image that there is a lasting property of the mathematical properties of sound and teh harmony of number.  Its not exactly "music of the spheres", but it does work. 

• 
  
  Good transliterated description are to be found on the Alchemy Website, here; the English-language version cane be found here.

Girdle vs. Goedel: the Pink Ice Girdle Ballet of 1951 vs. Logic. Part I of the History of Holding Things In

JF Ptak Science Books  

[My thanks to Patti Digh for providing the idea for the Goedel part of this adventure into Playtex and Logic--she did so because (a) they fit together and (b) girdle/Goedel sounded almost identical to a woman who once lived in Munich!]   

In the long history of Holding Things In, perhaps the newest of its members was upon us only recently. In the long, deep past we have held our breath, hidden our anger, stowed our emotions, and so on, but it was only recently that we began to hold our bellies in.  One of the masters of Holding Things In for this period turns out to be the sublime logician and re-inventor of modern mathematics (by putting one piece of the great Hilbert to sleep), Kurt Goedel, who towards the mistakenly-self-engineered end of his life, held on to everything, virtually--he organized and filed almost very piece of paper that he came into contact with at any level, became ever more reclusive, and at the end (due to his theories of people/institutions wanting to kill him) refused food and, of all things, water.  Surrounded by the smartest people on the planet (including his friends Einstein and von Neumann) up there at the Institute for Advanced Study at Princeton, Goedel withered away until he had almost no shadow. It is a bad irony that he could be so inconceivably unmovable and restrained while at the same time, and in the same life, offered such incredible newness to the maths--both ends of the mountain at the same time.

1951, the year in which these girdle advertisements appeared in Life magazine, was also the year that Goedel present us with the Goedel  metric, and also in which he received (with Julian Schwinger) the first Albert Einstein award (and of course delivered his famous Gibbs lecture  "Some basic theorems on the foundations of mathematics and their implications").

The popular introduction of the girdle I think that this happened at about the same time for the sexes, only these conveniences were much more often advertised for women than they were for men.  Slender and non-existent waistlines for women were more of a cultural identifier than a slim-hipped man, and the ads for his cheaters appeared far less frequently than those for women.

The first widespread appearance of the girdle for the sake of vanity must have occurred during the 19th century, or perhaps a little later is my best guess--but the first time the device began to appear for the common woman must've come around the time when there was time for leisure, or shopping, or of being seen in public in short intervals.  And that I believe is a Victorian-age invention.

But the binder doesn't come into fabulous presence until the distribution of mass population illustrated magazines, or I should say the advertisements that made these magazines possible:  production like LIFE (from which these 1951 images come) reached far more women than the popular older periodicals like Harper's Weekly or other polite mid-19th century journals for women.  The advertisements were certainly more enticing, the possibilities more rewarding, and the girdle comfort levels far higher than their predecessors, and the availability of disposable income for women far greater--and so incidentals like the girdle became more greatly commodified, and moved into the "essentials" category. 

The idea of these ads seem horribly revolutionary: on the one hand, the badly-named and hyphenated  Playtex product "Pink-Ice" squeezed women into new tight but  malleable molds, while at the same time promised some sort of ballet-like freedom because of it. Like the creeping ("two steps forward and one step back") communism of the time, Playtex promised the possibilities of enhanced freedom through restrictive clothing (in a "peace through strength" vision).  In any event, and in spite all of what I just wrote, the pictures are kind of amazing.  

[I'm well aware that this may be one of the worst things ever written about Kurt Goedel--the Renault Dauphine of Goedeliana.  But it doesn't matter, because in all of his powers, Goedel could absolutely prove that g_d existed, and that  I don't.]

Statistics as "Stutterings"; Dickens on People-Reduced-to-Numbers

JF Ptak Science Books   Quick Post

I found this in the Alex Cashman's lovely site, Mathematical Fiction (here). The except is from Charles Dicken's Hard Times (1854)¹, and in it we see Dickens making another in a long series of assaults on what he thought to be a disturbed social layering of dealing with the underclasses and the working poor.--and this time in the form of an entire novel. In the instance sited below (of interest right now because of its maths connection),  Dickens makes a case  for the"success" for the government of the fictitious city of Coketown to see a relatively small percentage of people in that city starving to death on its streets to be not a success at all. The character making the complaint is Sissy Jupe, whose fault at school came when asked the percentage of the starving/dying responded by saying it really didn't matter, because people were starving anyway, and whether it was one or a thousand dying from something as fixable as hunger meant all the same thing. She was presented with the "statistics"² from her teacher, but to Ms. Jupe it came to her ear as "stutterings", which is what Dickens felt the numbers were.  Dickens was attempting to make those people suffering in the streets less blank, less hollow, and more than a number.

Notes:

1.  It should be pointed out here that this is Dickens' 10th novel, the 42-year-old already having a enormous success with his writing and an even grater one in his storytelling. To this date, Dickens had already written The Posthumous Papers of the Pickwick Club (Monthly serial, April 1836 to November 1837; The Adventures of Oliver Twist (Monthly serial in Bentley's Miscellany, February 1837 to April 1839); The Life and Adventures of Nicholas Nickleby (Monthly serial, April 1838 to October 1839); The Old Curiosity Shop (Weekly serial in Master Humphrey's Clock, 25 April 1840, to 6 February 1841);  Barnaby Rudge: A Tale of the Riots of 'Eighty (Weekly serial in Master Humphrey's Clock, 13 February 1841, to 27 November 1841); A Christmas Carol (1843);The Chimes (1844);  The Cricket on the Hearth (1845); The Battle of Life (1846);The Haunted Man and the Ghost's Bargain (1848); The Life and Adventures of Martin Chuzzlewit (Monthly serial, January 1843 to July 1844);  Dombey and Son (Monthly serial, October 1846 to April 1848);David Copperfield (Monthly serial, May 1849 to November 1850); and Bleak House (Monthly serial, March 1852 to September 1853).  Remarkable.

2. "Statistics" as a word has been in use for a long time, finding air as early as 1787, at least so far as the sense in which it is used here. There are earlier references, but they actually refer to the "state", as in "statecraft" and government and such, and not for interpreting a collection of data.

The selection from Dickens below:

Reviewing Wells' "The Time Machine", June 1895, in NATURE

JF Ptak Science Books   Post 1859

I found this interesting 400-word bit in the 18 July 1895 issue of Nature (A Weekly Illustrated Journal of Science) and of course still very much alive and still a great publishing scientific powerhouse.  As Wells' treatment of time as a fourth dimension was still quite speculative, and his creation of the time machine as we now came from his hands, and as its reception by some literary journals was not very cordial, it is particularly interesting to see the positive review from this science journal.  As reported by Paul J. Nahin in Time Machines, Time Travel in Physics, Metaphysics and Science Fiction (published by Springer Verlag in a second edition in 1999, a graceful book of splendid observations with an introduction by Kip Thorne, Cal Tech's Feynman Professor of Theoretical Physics), Wells' book was seen as "hocus pocus"  and a "fanciful and lively dream" by  The Spectator and "bizarre" by the Daily Chronicle.

Nature's editors says of the book:

"...apart from its merits as a clever piece of imagination, the story is well worth the attention of the scientific reader, for the reason that it is based as far as possible on scientific data..."

"It is naturally in he domain of social and organic evolution that the imagination finds its greatest scope."

"From first to last the narrative never lapses into dullness."

And so Wells--who had cleaned up and rewritten an earlier version of this book from 1888--received a happy review from one of the leading scientific magazines of the time. It is not because of a wide interest of Wells in the fourth dimension per se that Wells wrote the book, but rather in rattling Victorian sniffy conceits of his day. 

*Time as the fourth dimension is a concept not much older than Well's idea, one of the earliest publications of the idea appearing ten years earlier (and written anonymously by "S") in Nature.  Charles Hinton, the person we most associate with the introduction of the fourth dimension  (or at least so on a popular level) didn't really establish time as the fourth dimension. (Hinton led a colorful, or at least interesting life--he was a brilliant guy, and also a convicted bigamist who was married to George Boole's daughter, and creator of an automatic baseball pitching machine. His books on the fourth dimension certainly were influential, and in the estimation of Florence was a contributor to the ideas of the coming modern art movements of the 1890-1910 period.)

And there were certainly many who came before Wells on the subject of the fourth dimension (though not many on the subject of time as the fourth dimension):  R.C. Archibald wrote on d'Alembert's (1754) use of time as a fourth dimension (in the Bulletin of the American Mathematical Society for May 1914); Cayley's "Analytical Geometry of n-Dimensions (Cambridge Mathematical Journal, 1843);  Grassmann's Die Lineale aus Dehnungslehre (1844); Riemann's 1854 effort on curved space (translated in 1873 for Nature by W. Kingdom CLifford); Beltrami's introduction of the pseudosphere in 1868;  J.J. Sylvester (again in Nature for 30 December 1869); Hermann von Helmholtz and his curvature for three-dimensional spaces; and Poincare's work in 1900, among others.  There is a rich field of these efforts, beautifully investgated for the general reader by Linda Dalrmple Henderson in her classic The Fourth Dimension and Non-Euclidean Geometry in Modern Art (Princeton 1983). 

Daily Dose of Dr. Odd: Arithmetic of 1935

JF Ptak Science Books   Quick Post 

Arithmetic of 1935 is an interesting book discussing the four prinipal operations of mathematics, though it is not quite Busby Berkeley's Gold Diggers of 1935.  It is however a very neat and orderly and in some ways exhaustive treatment of its subject, and that it does share with the brilliant choreography of Mr Berkeley. 

I've touched on Mr. Berkeley's work a couple of other times on this blog:  Bio-Mathematics in Busby Berkeley Musicals (here)  Mr. Mole, the Stationary Busby Berkeley of Mass Crowd Installation Photographs, 1918 (here).

Mathematical Sticks & Unmagic

JF Ptak Science Books  Quick Post

Just a quick post here on patented mathematical tools using long wooden planks in a sliding frenzy to find displayable answers for 19th century schoolchildren and their addition problems.  I know a good set of Napier's bone could come in very handy (appearing much earlier on than these instruments), but I'm just not sure what kids could learn from using these tools--like any other calculating device, early or late, they have a questionable quidity so far as appreciating the essence of numbers is concerned.   That said, the drawing for the Meyers' machine is beautiful, and could no doubt lead to a number of short, noir-y stories.

Source:  Google Patents, here.

Inventing Nothing: a Lovely Little Cipher, by Lewis Carroll

JF Ptak Science Books      Post 1807     Part of the series   The History of Blank, Empty and Missing Things

Lewis Carroll created a lovely, simple cipher in the midst of his Alice and Snark and Logic and Sylvie publications.  It really is just a simple bit of polyalphabetic substitution, bu tit gets the job done.  (Many others have walked this royal road:  Leon Battista Alberti, A Treatise on Ciphers, [De componendis cyfris];  Giovan Battista Belaso, La cifra del Sig. Giovan Battista Bel[l]aso, gentil’huomo bresciano, nuovamente da lui medesimo ridotta à grandissima brevità et perfettione, Venetia 1553 (and also his Novi et singolari modi di cifrare de l’eccellente dottore di legge Messer Giouan Battista Bellaso nobile bresciano, Lodovico Britannico, Brescia 1555); Giombatista Della Porta, De furtivis literarum notis vulgo de ziferis, G. M. Scoto, Neapoli 1563; Galileo Galilei, Intorno a due nuove scienze, Opere, . Vol. VIII, Firenze; Blaise de Vgenere, Traicté des chiffres ou secrètes manières d’escrire, Abel l’Angelier, Paris, 1586; and so on...its a very wide literature, even pre-18th century).  Louis Carroll. Louis "Cipher" Carroll.  Comes sort of goofily close to "Louis Cipher". Lucifer. Not the case, of course unless you were trying to figure out one of his tricky puzzles.

Perhaps it is the cipher's presentation and design and simplicity, its elegance, that I like so much.  It reminds me in some ways of the Henry Holiday masterpiece of nothignness created for Carroll's Hunting of the Snark--and that of course would be the Bellman's map, a map of nothing, a map showing nothing at all to the sailors who must follow it and who were all happy that the map had nothing to obstruct their vision of possibility and blank expectation. (I wrote about that in The Most Beautiful Map in the World, here). It is interesting to note that none of the illustrators who followed Holiday chose to illustrate the nothing map with such nothingness as in Carroll--there would be hands on it, or the map would be oblique, or not the central image of the illustration.  Holiday's map was just that--straightforward, simple, strong).

I've decided to make this a part of the History of Blank, Empty and Missing Things series simply because everything is missing unless you have the missing key--here you have all the parts of the puzzle, and then some, everything that you need to solve it, save for the integral part of ordering.

From Carrolls's text:

Explanation

Each column of this table forms a dictionary of symbols representing the alphabet: thus, in the A column, the symbol is the same as the letter represented; in the B column, A is represented by B, B by C, and so on.

To use the table, some word or sentence should be agreed on by two correspondents. This may be called the 'key-word', or 'key-sentence', and should be carried in the memory only.

In sending a message, write the key-word over it, letter for letter, repeating it as often as may be necessary: the letters of the key-word will indicate which column is to be used in translating each letter of the message, the symbols for which should be written underneath: then copy out the symbols only, and destroy the first paper. It will now be impossible for any one, ignorant of the key-word, to decipher the message, even with the help of the table.

For example, let the key-word be vigilance, and the message 'meet me on Tuesday evening at seven', the first paper will read as follows—

v i g i l a n c e v i g i l a n c e v i g i l a n c e v i
m e e t m e o n t u e s d a y e v e n i n g a t s e v e n
h m k b x e b p x p m y l l y r x i i q t o l t f g z z v

The second will contain only 'h m k b x e b p x p m y l l y r x i i q t o l t f g z z v'.

The receiver of the message can, by the same process, retranslate it into English.

If this table is lost, it can easily be written out from memory, by observing that the first symbol in each column is the same as the letter naming the column, and that they are continued downwards in alphabetical order. It would only be necessary to write out the particular columns required by the key-word, but such a paper would afford an adversary the means for discovering the key-word.