JF Ptak Science Books Revisting/Expanding Post #76 (from 2008)
Part I:
Nicholas Saunderson (1682-1739) was an extraordinary mathematical talent—he was also blind (from about the age of one), and invented, principally for his own uses, what I think is the first mathematical calculator designed specifically for the use of the blind.
He was supremely gifted and creative, and rose to become the fourth Lucasian professor at Cambridge, succeeding the expelled William Whiston, who had in turn succeeded Isaac Newton—Saunderson also held the post for one of the longest periods of time, 1711-1739. He was friend and associate to Newton, Whiston, Roger Cotes, Halley, De Moivre and others during a particularly rich intellectual period in the history of physics and the maths. 
His calculator was smart and simple, based on a cribbage-board –like device, that was able to perform arithmetical and algebraic functions—it consisted of nine rows and was worked with two pins, the positioning of the pins on the engraved board telling the user their value. (There was another calculator for the blind constructed by Meyer (below, left) using a sort of reverse principle to the Saunderson model where it was the shape and placement (leaning or not, for example) of the pegs in the hole that annotated value rather than their placement on the board.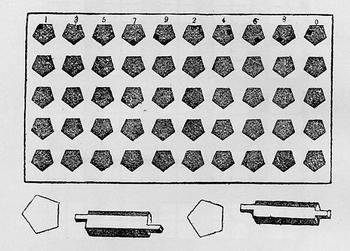 
The Saunderson computer was described in his The Elements of Algebra…, published at Cambridge in the first edition just after the author’s death, in 1740. The device was described in the book by John Colson (who succeeded Saunderson to the Lucasian chair), who commented that it was via the use of the device that
Saunderson could compose his treatise on algebra. (Above is another Saunderson-based calculator allowing for the construction and study of geometrical figures).
"Palpable Arithmetic", the sub-heading for the sheet illustrating aspects of algebra for Abraham Rees' (1743-1825) great if not problematic 45-volume Cyclopedia, is a system that records and organizes and sometimes calculates using three dimensional objects.
For example the Egyptians (for one) calculated with pebbles; then there was the ABAX of the Greeks, and the abacus (and also called the mensa Pythagoras) of the Romans (and of the Japanese and earlier still of the Chinese), the scaccarium of the English (via the Norman conquest), and innumerable other systems that performed arithmetic and recording and
archiving functions via the employment of reeds, notches on a tree or cloth or stick (etc.), reeds, knots, fingers, beans,shells, string, sand, and on and on. Palpable arithmetic also has a specialized meaning in places as a calculating device in which the numbers are recognized by touch and used by blind mathematicians or other parishioners. (Just for the record, there are a number of eminent blind mathematicians including, for example, Leonard Euler (1707–1783, who was blind in the last 17 years of his life), Nicholas Saunderson (who I wrote about in an earlier post), Louis Antoine (1888-1971), Lev Pontryagin (1908-1988.))
An interesting and very large philosophical issue that comes up here with the blind mathemaitican is the concept of image formation and its dependence upon sight for intuition, as with geometry or topology. Plato for one determined for himself that image formation issues were precognate and the same in sight and non sighted people. How would you manipulate a geometrical form if you’ve never actually seen one, or how would you extend you spatial imagination of compex forms without a reference?
But my main issue here is the image from the hees book. I'm by the meaning of this particular calculator or recording system--I just can't tell what it is. Can you? If so I'd love to hear from you.
Note on the Anthropology of Numbers:
From Levi Leonard Conant's The Number Concept Its Origin and Development we find these very descriptive definitions of words for numbers, all of which relate to the sort of implement that they were controlling
their numbers with, or calculating:
"in Javanese, Malay, and Manadu, the words for 1, which are respectively
siji, satu, and sabuah, signify 1 seed, 1 pebble, and 1 fruit
respectively. Words as natural and as much to be expected at the
beginning of a number scale as any finger name could possibly be. Among
almost all...the derivation of number words from these sources can constitute no ground
for surprise. The Marquesan word for 4 is pona, knot, from the practice
of tying breadfruit in knots of 4. The Maori 10 is tekau, bunch, or
parcel, from the counting of yams and fish by parcels of 10. The
Javanese call 25, lawe, a thread, or string; 50, ekat, a skein of
thread; 400, samas, a bit of gold; 800, domas, 2 bits of gold.The
Macassar and Butong term for 100 is bilangan, 1 tale or reckoning..."
The full sheet from the Rees book:
Comments