JF Ptak Science Books

When 2-D LOVE is 3-D LUST: Picturing another Spatial Dimension is Easier if you are Homer Simpson

JF Ptak Science Books   Post 1502

A note dragging together--against their will--the movie Hypercube, Homer Simpson, Marcel Duchamp, Jimmy  Neutron, Emile Jouffret, Filippo Marinetti, Paolo Uccello and Edwin Abbott.  Warning: this might not work.

We saw a movie the other night, Cube 2, Hypercube, which I think is meant to be Cube², but I honestly think that the title didn't appear that way because not that many people (?!) would know how to "pronounce" the little superscript floaty "2".  The movie was pretty interesting, telling the story of a group of people "imprisoned" in a large, sterile cube with a door on each face that opened into an identical cube, and on and on into a Borgesian infinity-hell.  At one point the people are theorizing on the nature of the Cube, winding up with someone saying that they might all be in a fourth spatial dimension. 

It brings up a pretty well-worn thought about visualizing a different dimension, and then it occurred to me that the only general-population folks who seemed to be most at ease with this idea were cartoon characters: and since I am a father of children, a Father of Children, I am very well familiar with recent cartoon history.  Homer Simpson, for example, slips from his two-dimensional world into what was supposed to a three dimensional world, and he seems perfectly comfortable.  (The equation in the background, 1782^12 + 1841^12 = 1922 ^12 is correct for the first nine digits, but not for the last thirty.  Plus, since the product of odds is odd, and the product of evens are even, the sum of even and odds is odd, so the answer must be wrong. But close.  And really, really good for little Homer.) Timmy Turner (Fairly Oddparents) and Jimmy Neutron (of the show bearing his name) switch worlds,one going 2-to-3 D and the other the other way 'round, with both being perfectly comfortable in their new space.

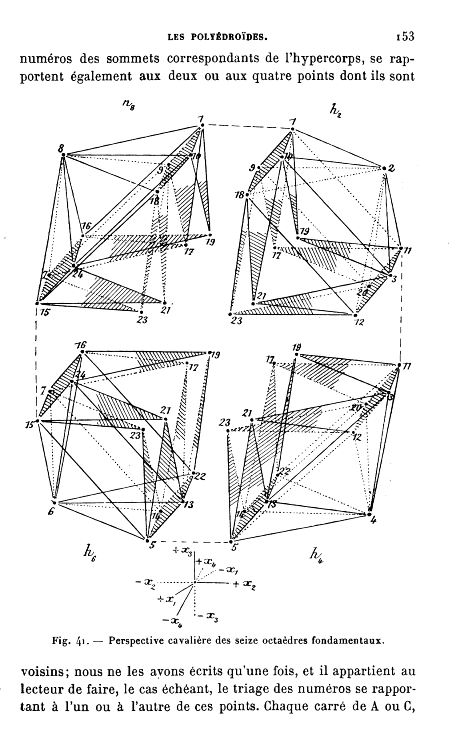Of course the issue of imagining a three-dimensional shape in a two-dimensional world is pretty knotty if you are not having a cartoonist draw out your brain's interpretations of the world.  The great classic of this is Edwin Abbott's Flatland, an 1884 book about a two dimensional world of shapes that encounters a dot that grew concentrically and outwardly, a dot expanding and then contracting itself in a series of circles, morphing until it appeared as a new and revolutionary form rising from the plane of Flatland, evolving into a new thing, a Sphere.  The folks in Flatland had a hard time with it.

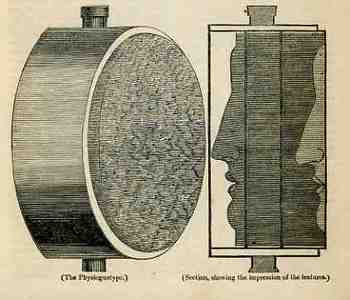Depicting a third dimension in a two-dimensional space is tough, the whole deal being rediscovered in perspective only relatively recently in the history of human thought, being only about 600+ years old. (In quasi order perspective is brought to the West by Cimabue, the Isaac Master, Giotto, Duccio, Maso, Avanzo, Lorenzetti, Donatello, Ghiberti, Fra Angelico, and so on, not the least of whom would include our beautiful Paolo Uccello.)  Giving real "flavor" to the extra dimension was still quite difficult, even in the 19th century.  In the “Spirit of Discovery” section of the British weekly magazine The Mirrour of Literature, Amusement, and Instruction for 22 October 1836 there is a short notice on the “physiognotype”, “a machine for taking casts, lately invented by a gentleman in Paris”.  We’re accustomed to these devices now as they’ve been for sale in toy shops for decades—but in 1836 it was a real breakthrough for making instantaneous three-dimensional models of small things.  In 1836 there really wasn’t any simple way of producing a direct, proportional model like this in 3-D except for encasing it in plaster and then casting from that mold.  Two-dimensional modeling was easier, and there were numerous devices constructed for this purpose as people pursued the still-hot rage of physiognomic forecasting, with simpler means (like shadow portraits) being hundreds of years earlier.  (Photography remember is still three years away from being announced and another few years from being sort of accessible to middle-class folks.)

Imaging the fourth dimension was more a product of mathematics than of art, with people like Emile Jouffret¹ getting to it a little before Marinetti and Duchamp and the squirrely Picasso did. (Thinking on the fourth dimension goes back as far as Kant, at least, and the real work begins in the first half of the 19th century².)

  But it seems as though the cartoon (like Homer, above) and comic book characters have a much easier time with this added-dimension issue, using it to full advantage without muss or fuss, and certainly without any philosophical commentary.  Their reach across the aisles of the 1952 Rexalls and other general merchandise emporia  with enough floor space for a revolving magazine stand was straight into the heart of the common reader, filling them with the hope/fear of their two-dimensional explorations into what they called their 3-D  3D  3.D  Three Dee world, selling "closer-to-life stories in closer-to-life 3rd Dimension". 

It seems that the same might be true for 3-D movies as well, the characters busting out into a new dimension (sometime fully aware of it) without a care or riddle, the main effect of finding the new spatial dimension sitting squarely in the minds of the observers, who are already in that dimension and reacting to somethingf with a surprising surprise of seeing a familiar thing in its proper context.

I'd love to know what that fourth spatial dimension looks like, as promised by The Starlets...or maybe not.

Notes:

1. Jouffret, E.  Traite Elementaire de Geometrie a Quartre Dimensions et Introduction a la Geometrie a n-Dimensions. Paris:  Gauthier-Villars,  1903.  1st edition. ! 215pp. and   Jouffret. Melanges de Geometrie a Quatre Dimensions.   220pp. Paris:  Gauthier-Villars,  1906.  1st edition. (Perhaps one of the most classic works of the late 19th and early 20th c on imaging the fourth dimension--certainly well known to the Cubists and Futurists, I'm certain that it sparked any number of ideas in the art world.)

2. The first major work arrives with Hermann Grassmann's "Die Lineale Ausdehnungdlehre" (Theory of Linear Extensions) in 1844 (and the subsequent translations of the work as well as original work by Arthur Cayley); followed by Ludwig Shclafli (1814-1895) "Theorie der vier flachen...." (Theory of Continuous Manifolds, 1852 but not published until 1906), Riemann's 1854 speech (which was not published until 1867 and which appeared translated by William Kingdom Clifford in Nature in 1873, G.F. Rodwells "On Space of Four Dimensions" (Nature, May 1873),  Dodgson/Carroll's  Through the Looking Glass (1872) deep references, Zollner "On Space of Four Dimensions"

Strange Things in the Sky Department: the Sky-borne Seat of All Wisdom in the 12th century

JF Ptak Science Books   Post 1486

Hildegard of Bingen (ca. 1098-1179) was a polymathic religious visionary¹, composer and writer who was a well-know intellectual whose work attracted the attention of people at all levels, not the least of which were several popes  In one version of the manuscript of her 150,000-word work, Scivias (Scito vias Domini, or "Know the Ways of the Lord" ) we find the following illumination, which is basically an image of the object that contains the nameless stuff of the human soul:

The image above—from the Wiesbaden manuscript and unfortunately only in a black-and-white, and found in Charles Singer's From Magic to Science (1928)²--shows Hildegard's vision of the soul entering the body. (There's a wide range of opinion concerning how much influence Hildegard had on these images—some say that she sketched out the outlines, or directed the illuminator, or had some sort of hand in the construction of the image, all with varying levels of involvement.³)

It is an extraordinary thing, trying to represent what gives the human-ness to people as seen from a 12th-century perspective, and in Hildegard's version/vision it is the soul, the very essence of the birth and death cycle of human nature.  It is resident as we see within a special place in the sky, the "the wisdom of god" (Singer page 226), and it passes from the vault of heaven into the fetus while still within the mother's womb.  It is in this square, evidently, that the essential matter of the creator can be found, and within that structure can be seen the essence of the stuff of human nature that is about to pass into the developing fetus through the tube-like connection. As Singer writes, quoting (loosely?) from the manuscript: "down this [the tube] there passes into the child a bright object, described variously as 'spherical' and as 'shapeless' which 'illuminates the whole body' and becomes or developes into the soul." (Singer, p. 226).

In the frontispiece to another ms of Scivias, we see Hildegard herself sitting and making a sketch on a wax tablet (a sort of Medieval chapbook, or hornbook, or slate/charcoal sketchpad that could be reused), showing that the images she created were the product of a higher source, of light from another metaphoric vault:

Notes

1. Hildegard said that she had these vision,s from a very early age, beginning at about 3.

2. This manuscript was removed from Wiesbaden during WWII and “sent to Dresden for safekeeping”, where it subsequently “disappeared”. “Destroyed” is more like it, as Dresden of course was the scene of an enormous firebombing campaign in the last days of the German involvement of WWII. There are still hopes that the ms lives somewhere in someone's grandfather's attic, perhaps taken in the third week of February 1945 as war booty, and then forgotten. "You guys burnt the place down, turned it into a single column of flame. More people died there in the firestorm, in that one big flame, than died in Hiroshima and Nagasaki combined." --Kurt Vonnegut, Jr

3. Historian of science Charles Singer and medical anomaly writer Oliver Sacks have both made strong cases for Hildegard to have been a migraine sufferer, though they do explicitly state that given that as the case it does not necessarily affect the vision that she had.

As found in the Wikiu article on Scivias:" Some authors, such as Charles Singer, have suggested that the characteristics of the descriptions of the visions and the illustrations, such as bright lights and auras, imply they may have been caused by scintillating scotoma, a migraine condition.[25] Oliver Sacks, in his book Migraine, called her visions "indisputably migrainous,"[26] but stated that this does not invalidate her visions, because it is what one does with a psychological condition that is important.[27] The resemblance of the illuminations to typical symptoms of migraine attacks, especially in cases where it is not precisely described in the text, is one of the stronger arguments that Hildegard herself was directly involved in their creation.[28]

It has also been suggested that the visions may have been due to hallucinogenic components present in ergot, common in that area of the Rhineland, at certain times of the year.[29]”

The contents of Scivitas:

 

A Square of Horse--Naming Groups of Animals ("A Murder of Crows", continued)

Aelianus (Tacitus) The Tactiks of Aelian Or the art of embattailing an army after ye Grecian manner. Englished & illustrated with figures throughout & notes upon ye chapters of ye ordinary motions of ye Plalange by J.B...  

The “J.B.” here is the author John Bingham, whose book was published in 1616. The "Square of Horses” seems to me to be a fine addition to a named bestiary, in addition to a "murder" of crows and an "unkindness" of ravens (and a "crush" of rhinos, and on and on, as we can see below). 

Names given the collectives or gatherings or units of animals are useful and informative, and occasionally fabulous and bizarre.  It seems to me that such characterizations could be made with people as well,  Why should humans have such a uniform label for collective employment members (a “group” of lawyers, a “gathering” of architects, and so on) when animals have such a rich vocabulary to draw from?  Admitedly, animals don’t go out and get lawyers when they feel maligned by a broadly advanced descriptor, so there’s little chance that more appropriate upfittings could be applied to different job classifications.  Unless of course you consider the “managed corporate associate monetary inventorialist” (cashier) as an example—but that is not what I’m talking about. 

In the animal world, for example, a group of gorillas is a simple “band”, chicks a “clutch”, and quail a “covey”, which is simple enough.  The names get more adventurous as things progress in the food chain:  hippos are a “bloat”, a word which seems to identify a characteristic of the animal, especially when they’re half-submerged, watching the sun move across the sky with their eyes just above the waterline..  Ferrets are a “business”, semi-inscrutable in their nervous activity. Hyenas are a “cackle”, hawks are a “boil” and finches are a “charm”.

A group of rhinos are beautifully referred to as a “crash”, and squirrels are poetically announced as a “scurry”

Perhaps the second greatest of all of these names is that for a gathering of crows, called a “murder”.  It is probably the crow which, among all animals, may be the only one “smart” enough to commit the crime—it is an undoubtedly intelligent animal, with a brain-to-body mass ratio third to that of humans (behind apes) and have been shown to work in concert with one another toward a common end, and have also used tools in the pursuit of food.  They have also been depicted for thousands of years in mythology and story as intelligent, crafty creatures.  My choice for the most fabulously-named:  an “unkindness” of ravens.   These birds enjoy a similar heritage to the crow, but have a greater literary heritage.  Unkindness and Poe seem to go together quite nicely. 

A leap of leopards, a gulp of cormorants, a romp of otters, a parliament of owls.  An ostentation of peacocks, a prickle of porcupines, a stand of flamingoes, a pride of lions, a wake of buzzards, a tower of giraffes: all seem to fit quite nicely. 

What would the human equivalent be?   A "grotesque" or a "provident" of attorneys,  a "shushing" or "shepherding" of librarians, a "scribble" or "release" of writers, an "envy" or "relief" of actors?  I think it needs to be Latin and deep for the politicians.  Very deep. 

(A directory of names follows in the continued reading section)

 

 

A band	Gorillas
A bevy, covey	Quail
A bevy, wedge (in flight)	Swans
A bloat	Hippopotamuses
A brace, flock (in flight), raft (on water) team, paddling (on water), badling	Ducks
A brood; clutch	Chicks (of many species)
A building	Rooks
A business	Ferrets
A cackle	Hyenas
A cast, kettle (flying in large numbers), boil (two or more spiraling in flight)	Hawks
A cete	Badgers
A chain	Bobolinks
A charm	Finches
A clowder, a pounce; for kittens...A kindle, litter, an intrigue	Cats
A colony	Bats
A colony	Gulls
A colony	Penguins
A colony, warren, nest, herd (domestic only), litter (young); specific to hares...A down, husk	Rabbits
A company	Parrots
A company	Widgeons
A congregation, wing (in flight)	Plovers
A convocation	Eagles
A cover	Coots
A covey	Partridge
A covey	Ptarmigans
A crash	Rhinoceroses
A deceit	Lapwings
A descent	Woodpeckers
A dray, scurry	Squirrels
A drift, drove, litter (young), sounder (of swine), team, passel (of hogs), singular (refers to a group of boars)	Pigs
A drove, flock, herd	Sheep
A drove, herd	Cattle
A dule, pitying (specific to turtle doves)	Doves
A fall	Woodcocks
A flight	Swallows
A flock, gaggle (on the ground), skein (in flight)	Geese
A gang	Elk
A gang, an obstinacy (I suspect these refer to old world buffalo; use "herd" for American bison)	Buffalo
A gulp	Cormorants
A herd	Elephants
A herd, bevy (refers only to roe deer)	Deer
A host	Sparrows
A labor	Moles
A leap	Leopards
A leash, skulk, earth	Fox
A litter (young), pack (wild), cowardice (of curs); specific to hounds...A cry, mute, pack, kennel	Dogs
A murder, horde	Crows
A murmuration	Starlings
A muster, an ostentation	Peacocks
A mustering	Storks
A nest, nide (a brood), nye, bouquet	Pheasant
A pace	Asses
A pack (in late season)	Grouse
A pack, rout or route (when in movement)	Wolves
A pack, span, barren	Mules
A parliament	Owls
A party, scold	Jays
A pod, gam, herd	Whales
A pod, herd	Seals
A prickle	Porcupines
A pride	Lions
A rafter, gang	Turkeys
A richness	Martens
A romp	Otters
A sedge	Bitterns
A sedge	Cranes
A sedge, a siege	Herons
A Shrewdness	Apes
A sloth, sleuth	Bears
A sord (in flight), brace	Mallards
A spring	Teal
A stand	Flamingos
A streak	Tigers
A team, harras, rag (for colts), stud (a group of horses belonging to a single owner, string (ponies)	Horses
A team, yoke	Oxen
A tiding, gulp, murder, charm	Magpies
A tower	Giraffes
A tribe, trip	Goats
A trip	Dotterel
A troop	Kangaroos
A troop, barrel	Monkeys
A wake	Buzzards
A walk, a wisp	Snipe
A watch	Nightingales
An exaltation	Larks
An unkindness	Ravens

 

The Problem of the Expanding Universe, 1943

JF Ptak Science Books    Post 1368

In his great summary (The Problem of the Expanding Universe) of the development of the velocity-distance relation, the Big Bang and all that,  Edwin Hubble offers concise appraisal of the research to this point (in which Hubble and his assistant Milton Humason were prominent members of its founding studies). Hubble provided the first experimental data supporting the expanding universe theory of Georges Lemaitre's cosmology (the "hypothesis of the primeval atom"), Einstein's GRT and the mathematical equations of Alex. Friedmann, finding that the distance of galaxies were proportional to their redshifts (Hubble's Law, 1929).  The whole thing enjoyed a bigger, more explosive life once it had been given its  more provocative and user-friendly name by Sir Fred Hoyle, who called the idea "the Big Bang" in 1949.  (Sir Fred was actually attacking the idea and must've thought his tag was to be demeaning, but as a proponent of the steady state theory, Hoyle's plan backfired, a proof that irony exists.) The steady state model was more or less put to sleep when the cosmic microwave background radiation (first proposed by George Gamow, Ralph Alpher and Robert Herman in 1939) was "discovered " in 1964 by Penzias and Wilson, this providing further experimental confirmation for the Big Bang hypothesis. 

In his characteristic way, Hubble summarized the whole package so, in the conclusion of the 13-page paper [the original of which is available for purchase from our blog bookstore]:

"Meanwhile, on the basis of the evidence now available, apparent discrepancies between theory and observation must be recognized. A choice is presented, as once before in the days of Copernicus, between a strangely small, finite universe and a sensibly infinite universe plus a new principle of nature."

It is an excellent approximation for a semi-general-public speech (to the Smithsonian Institution crowd during the war in 1943), and reminds me of one of his other, similarly spot-on statements, one of the greatest understatements in 20th century astrophysics The statement appears in a further report on Hubble/Humason studies in The Velocity-Distance Relation Among Extra-Galactic Nebulae  (Mount Wilson Observatory,  1931) ,  a regarding their understanding of the phenomena and the expanding universe, the authors take many steps back, and say in the concluding paragraph:

"...the writers are constrained to describe the apparent velocity-distance displacements without venturing on the interpretation and its cosmological significance".

They basically lay out the functioning of the universe and the best understanding of how we got to where we are in the cosmos (Vesto Slipher notwithstanding), and how according to their understanding that the universe is expanding and is consistent with all known laws, that they decide to not say anything, um, philosophical, in the light of disrupting the idea of the creation of all things.

Hubble did have a way with words, his own way, though he was able to communicate a difficult series of ideas simply, as we can see in the opening of his Expanding Universe paper: 

"Mathematicians deal with possible worlds, with an infinite number of logically consistent systems. Observers explore the one particular world we inhabit. Between the two stands the theorist He studies possible worlds but only those which are compatible with the information furnished by observers. In other words, theory attempts to segregate the minimum number of possible worlds which must include the actual world we inhabit. Then the observer, with new factual information, attempts to reduce the list still further. And so it goes, observation and theory advancing together toward the common goal of science, knowledge of the structure and behavior of the physical universe."

And this lovely summation:

"Current theory starts with two fundamental principles : general relativity and the cosmological principle. General relativity states that the geometry of space is determined by the contents of space, and formulates the nature of the relation. Crudely put, the principle states that space is curved in the vicinity of matter, and that the amount of curvature depends upon the amount of matter. Because of the irregular distribution of matter in our world, the small scale structure of space is highly complex. However, if the universe is sufficiently homogeneous on the large scale, we may adopt a general curvature for the universe, or for the observable region as a whole, just as we speak of the general curvature of the earth's surface, disregarding the mountains and ocean basins. The nature of the spatial curvature, whether it is positive or negative, and the numerical value, is a subject for empirical investigation."

"The second, or cosmological principle is a pure assumption – the very simple postulate that, on the grand scale, the universe will appear much the same from whatever position it may be explored. In other words, there is no favored position in the universe, no center, no boundaries. If we, on the earth, see the universe expanding in all directions, then any other observer, no matter where he is located, will also see the universe expanding in the same manner. The postulate, it may be added, implies that, on the grand scale, the universe is homogeneous and isotropic – very much the same everywhere and in all directions."

"Modern cosmological theory attempts to describe the types of universes that are compatible with the two principles, general relativity and the cosmological principle. Profound analysis of the problem leads to the following conclusions. Such universes are unstable. They might be momentarily in equilibrium, but the slightest internal disturbance would destroy the balance, and disturbances must occur. Therefore, these possible worlds are not stationary. They are, in general, either contracting or expanding, although theory in its present form does not indicate either the direction of change or the rate of change. At this point, the theorist turned to the reports of the observers. The empirical law of red shifts was accepted as visible evidence that the universe is expanding in a particular manner and at a known rate. This arose the conception of homogeneous expanding universe of general relativity."

I like Hubble.

Notes:

The paper begins:

"I PROPOSE to discuss the problem of the expanding universe from the observational point of view. The fact that such a venture is permissible is emphatic evidence that empirical research has definitely entered the field of cosmology. The exploration of space has swept outward in successive waves, first, through the system of the planets, then, through the stellar system, and, finally, into the realm of the nebulae. Today we study a region of space so vast and so homogeneous that it may well be a fair sample of the universe. At any rate, we are justified in adopting the assumption as a working hypothesis and attempting to infer the nature of the universe from the observed characteristics of the sample. One phase of this ambitious project is the observational test of the current theory of the expanding universes of general relativity. " [The entire paper is located here.]

Elements for a Whiskey Alphabet Drawn from the Bible of Booze Names

JF Ptak Science Books  Post  1363

It may or may no be the case, but this large, flaking book that is balanced on top of a petulant pile of paper, Registered Beverage Trade Marks Covering the Period from 1881 to 1939 Compiled from the records in the United States Patent Office (Distilled Alcoholic Liquors) may be the keys to the kingdom of names of booze(s) trademarked in this country.  15" tall, and inch thick, and 296 sheets big, this work (copyrighted y the Trade Mark records Bureau (in the National Press Club Building in DC, the one with the problematic parking garage) lists some 7,500 names of whiskey, cordials, gin, rye, bourbon and who knows what else.  I cannot find the book in any online database, big or small, and I'm not sure where this info might be housed and housed in one spot.  I have no doubt that people somewhere need this data, unwieldy and unusable as it might be--you see, it is organized only according to a six/seven digit number which I guess is the trademark filing number, or something; there is nothing else useful about the thing, the data floating around without regard to year or place or liquor type. [The book is available from our blog bookstore, here.]

So I sat down with the book for an hour pulling out interesting, odd, out-of-place, from-another time and bizarre names, including all manner of expected animal names like bull and elk, and then unicorn; and lots of sunny this-and-that, sloping/sunny/grassy hills, mountains, clubs; and of course the Old _____  category seem fairly filled up. 

If I spent a little more time on this entire alphabets could be produced relating to nothing but names from the animal kingdom, flora, the sciences, professions, religion, states of mind, altered states,  literature, and the labels that suggest a possible medical benefit.  One of my favorite categories is the "conversational liquor label", the label that speaks to you, invites you, tells you what to do with the bottle of booze:  Hava Cocktail and Uneeda Whiskey are good examples of that, as are You're Lookin Good, Uvanta and Yugeta whiskeys. Another is the liquor name ending in "o", like the beautiful Famo, from St. Jo, MO, which unfortunately wasn't trademarked in '00.  The label of suggested promise and outcome is another good one:  Kentucky Courage, Pleasant Dreams, Invincible Rye, Solace Whiskey and Ready Money are all good examples of the implied end-of-bottle pillow-fluffer...maybe, especially, The Old Solution whiskey.

And then of course, there are those where the (creative) spirit has just flown away, like the lumpily-named Standard Spirits Whiskey, its hometown of New Orleans embarrassed by the lack of effort--especially in the light of some many hundreds of imaginative creations, like the fabulous Bone Factor Whiskey (1903), which like som many other great names  (Yellow Hammer Whiskey) comes from Louisville, Kentucky.

Antediluvium Whiskey, NYC, 1898; Anti-Grippine Whiskey, Philadelphia, 1906; Ash Cake Whiskey, Lynchburg, VA. 1899, Auto Crat Whiskey (St. Louis, MO), 1905

Bank Check Whiskey, Boston, 1900; Bone Factor, 1903;

Caloric Whiskey, 1904; Cremo Whiskey, 1902; and the confusing Chickencock "potable spirits", 1929

Devil's Island Benefactor Gin, 1905; Daily Mash Whiskey, 1935; Dandilyon Whiskey, Columbus, OH, 1906;

Electric Whiskey, Cincinnati, 1890;

Flow Whiskey, Pittsburgh, 1908; Famo Whiskey, St. Jo, Mo 1894; Faust's Own Whiskey,  Phila, 1900.

Gopher Gin, St. Paul, 1902; Gas Away, Columbus OH, 1902; Galoxy Whiskey, NYC, 1905; Gong "ethyl alcohol, etc," 1932' Georgia Watermelon, 1911

Hen Bolt Whiskey, 1889;  Hava Cocktail, NYC, 1933; Hospitality Gin, Louisville, KY, 1900

Index Whiskey, Cincinnati, 1906; Invincible Rye, 1900

Jupiter Gin, Boston, 1905; Judge's Preference, Boston, 1905;

Kentucky Courage Whiskey, Lexington, 1900

Marconi Whiskey, Birmingham, 1903

Old Tom Gin, 1887 (There are any number of Old ____ labels: Old Crow, Old Man River, Old Count, Old Court, Old Coon, Old King Cole, Old Rock, Old Moss, Old Soldier, and so on--there's a specialized sub-alphabet in this category, alone.)  Perhaps my favorite "old" is The Old Solution, Baltimore, 1900.

Peeper Whiskey, Lexington, KY, 1880; Pen and Pencil Club Rye, Phila, 1894; Pleasant Dreams Whiskey

Radium Whiskey, Terre Haute, 1905; Rolling Fork Whiskey, Lexington, KY, 1876; Ready Money Whiskey

Sun Shot Cordial, Birmingham, AL, 1901; [SWASTIKA emblem, no name] Whiskey, Frankfort, KY,  1902; Suburban Whiskey, Boston, 1909; Solace Whiskey, Balto, 1900

Tidal Wave Whiskey, Houston, 1905

Uncle Tom Whiskey, Cincinnati, 1905; Uneedda Whiskey, Davenport IA, 1899;  Uvanta Whiskey, Louisville, KY, 1905

Vitoline Brandy,  St. Paul, 1897

Yugeta Whiskey, Plymouth, PA, 1906; You're Lookin Good Whiskey, D.C., 1902; Yellow Hammer Whiskey, Louisville, 1905

Zeno, Ace of  Clubs Whiskey

And to sew up the specialty market in school-named liquors, Lawrence McCormick of Baltimore trademarked whiskey names for Brown, Yale, Harvard, Princeton, Cambridge, Cornell, Swarthmore, Chicago, Oxford and of course Lehigh University, not to mention various label designs that featured books and "philosophical instruments" emblazoned on shields and rocks and such, all perhaps for those in search of higher education.

Unfortunately there are no images of the labels in the book, though I guess if someone could find 200 or so they'd have themselves a snappy coffee table book of their own. 

 

 

 

Contrary Big Crowds Series--a Chaos of Hats and an Order of Heads with No Hats

JF Ptak Science Books--Quick Post

Coming upon this image of a sea of hats, which in the fine tradition of naming collections of self-similar things-like a gaggle of geese or a murder of crows--a 'Chaos" of Hats, I needed to find its contrary, and a relatively orderly and ordinary one at that. [I compiled a list of  oddly-named groups in an earlier post here called An Unkindness of Ravens and a Murder of Crows.]

What better than an Order of Heads?  This image is of a church or social service at Pentonville Prison in 1855.  The penitentiary engraving is real;  but the  truth be told,  the Chaos photo is a manipulated image, about a half of the original of something I made, mainly because I just wanted to see  a very hatty crowd around the man in the middle pointing at the camera. 

As it turns out, Pentonville--serving North London loyally since 1816, and still doing so--was the home for a bit of Oscar Wilde and Boy George.  It was also the place where Arthur Koestler began composing his thoughts for his magnificent Darkness at Noon.

Reading Symbolism in Raymond Lull's Portrait

JF Ptak Science Books  Post 1333

Raymon Lull is perhaps the most famous Catalan given to the world--he is also one of the most famous people in history with the most names. (He was also known as Ramon, Raimundo and Raymond, Raimundus and Raymundus Lull, Lully, Llull, and Lullus and Lulio, among others.) Seriously though, he was a very interesting thinker who went far beyond the norm, and then some, his creativity overmatching the possibilities of the parenthetical sciences of his time, and stretching timeless logic as well as he went along.  But so it goes, as they say; he did do aggressive work and at the very least it was for the most part quite pretty-sounding.  And as he pushed up and against existing thinking it was up to that confronted thinking to push back--which sometimes happened and sometimes didn't. He studied the law, alchemy, botany, religions, and may well have written the first novel ever to appear in Europe (at least it was the first in Catalan)--I think that you could say, overall, that he was a rationalist. 

• The original engraving is available at the blog's bookstore, here. 

This engraving is one version of many that I've seen online, and may be the original--this is a pure guess on my part, my reasoning is so mainly because there is so much more added detail than in any other versions of the engraving.  the added bits in the corners, and of course the scene revealed by the pulled-back curtain.  The engraved lines are also very sharp, very pronounced, not like some of the other version which look a little less defined...this one is razor sharp. (The image is available for purchase from our blog bookstore.)

The word balloon (and by the way I wrote a post here two years ago on the history of word balloons) coming from Lull's mouth is Lux mea est ipse dominius "My light is that of the Lord", a claim for divine inspiration, guidance, fortitude.  Beyond all else Lull was a Christian, and a Christian to some severe fault--he was very involved in the conversion of Muslims, and was also an (utter) expulsioist in regards to the Jews.  The Christian philosophies of Lull are clearly shown in this 17th century portrait of the man. 

And in the scene that is not seen in the other reproductions of this portrait online we see a small host of interesting sci-philosophical instruments cluttered around what seems to be a giant working with an astrolabe.  (This fellow is a head taller than the other people gathered around him, and he is most definitely sitting down on a high stool, making him taller still.)  We see dividers and various measuring devices, plotting instruments, and even a pair of specs, which would've been very uncommon in in the 13th century.  I'm happy to see a dog sleeping through the ruckus.

In the sky in place of the sun is a triangular collection of burning candles, or they seem like candles, which continues a very old tradition of symbolizing unity, and in this case, in  a Christian theme, a god surrounded by the holy trinity... related symbols appear frequently in images depicting the Old Testament creation cycle. 

 

Continuing this theme, if you look in the right upper corner of the engraving there is another interesting symbol--a hand issuing from a cloud with a book, sourounded by three fleur de lis.  This is in obvious reference to the balloon statement, the hand of god issuing a book, or knowledge, to the recipient (which would be the reader or Lull); the fleur de lis, a French lily, was often used in Renaissance and Baroque imaging as a representation of the holy trinity, and of purity and chastity, spirituality.  Or  perhaps it was just a flower. 

 My own interest in Lull--aside from the  great beauty in which his ideas were encapsulated and presented--is in his idea generator, and the possible influence it had on later thinkers like Leibniz who may have built on his interesting breakthrough to produce one of the earliest arithmetical calculators.  Lull's own calculator (which I wrote a little about here) is simple and elegant, and may actually be powerful for some--it was a series of discs that when turned would relate ideas and letters and numbers which were by serendipity intended to generate unexpected ideas to think about.  For the 13th century this was a major idea, and I like it even today. 

 

                          

Warsaw Ghetto Uprising--Full Text of a Rare 1944 Pamphlet

JF Ptak Science Books  Post 1294

"There will be a dawn."--Dorothy Thompson, 1943

"The former Jewish quarter in Warsaw is no longer in existence”--Jurgen Stroop, liquidator of the Warsaw Ghetto.

Dorothy Thompson got that one wrong--or so at least got the "dawn" wrong when it comes to the Jewish uprising in the Warsaw Ghetto in 1943.  There wouldn't be a dawn, there, mainly because there would be hardly any Jews, or Warsaw.  [This battle took place about three years after the Nazis established it as a means of control for the city’s 400,000 or so Jews. In the intermediary years hundreds of thousands of Jews had been “deported” (that is, sent to the concentration camps to be exterminated or worked to death), so that by the time of the Uprising only 60,000 people remained in the Ghetto.  And by this time there was no doubt in anyone’s mind who lived there (and perhaps too in Warsaw as a whole) what the euphemism of “deportation” actually meant.  The battle started off well for the home defence (the ZOB) but, ultimately, with little access to resource and with nowhere to actually retreat or regroup in the few acres that remained of the original Ghetto, whoever was left in the Ghetto were either killed or captured by 16 May.  The German commander, SS Brigadefuhrer Jurgen Stroop reported on that day that “the former Jewish quarter in Warsaw is no longer in existence”.]

This small pamphlet was written by Reca stone in 1944 on the Jewish counter-attack against the Nazis in the ghetto of Warsaw. It is one of not-many that documented not only the resistance in Warsaw, but also of the wholesale liquidation going on in that city and in the concentration camps. in general.  (Again, this was written in 1944. )

There weren't many accounts like this, but there were enough, certainly enough to have made a difference, I think, in how the leaders of the war effort approached whether concentration camps existed or not.  Franklin Roosevelt had exactly one meeting on this topic (which I wrote about here), while many others decided that the idea of exterminating all of European Jewry was so enormously bad and so gigantic that it could not possibly be true.  

Felix Frankfurter famously replied to a first-hand report on the extermination from the great Jan Karski that he just couldn't "beieve" Karski's story--not because the Supreme Court Justice (and Jew)  thought Karski wasn't telling the truth, just that the story itself was unbelievable.  And whether people thought that the stories were the truth but unbelievable (like Frankfurter) , or whether they thought they to be exaggerations, or whether they thought it was impossible, the responses and the subsequent actions mostly seem to have come to the same end of nothingness. Even after years of reports of extermination and brutalities and millions of people missing (as FDR was warned of in that 1942 meeting), the actual eyewitness accounts of the concentration camps were still received as being unbelievable.

This is one of the reasons why General Eisenhower--when viewing the  concentration camp at Ohrduf in April 1945 with Generals Patton and Bradley--suggested that world leaders and other high-rankers come to the camps to bear witness so that future generations would know that such a thing actually existed.  And so we come to the Reca Stone pamphlet.  There are many other accounts of course of the uprising, and many of those are available on-line--but the Stone account, which is a rare thing in itself (only seven libraries worldwide having a copy of the work) is not on-line, but it is now.  I think that it is a significant report, and it should have a wide audience--things like this should reach as large a readership as is possible. 

An example of Stone's reporting, coming from Underground sources and the Polish Jewish Reporter, on the number of Jews "removed" from the Ghetto of Warsaw between July 22 1942 and September 21, 1942--254,954 over a period of about three months:

But Stone gives no sentiment to the idea of Jews "perishing".  On page 20 she describes the death camp Treblinka, and how thousands and thousands of Jews met their death in the gas chambers, or by suffocation and scalding, or by execution, or by live burial.  

She writes boldly: In this manner 250,000 Jews were transported from the Warsaw Ghetto...and in this manner tjhey met their death".  Period.  No euphemism here.

She also quotes Washington sources that "two million" Jews had "perished" (the Federal term, not Stone's), and that "five millions were imminently threatened with death".  She pretty much got everything correct, as unbelievable as it sounded, then.  Or now.  

 

The original pamphlet is available for purchase here.

The full test, below--all of the images are expandable:

Jackson Pollock's Fractals

JF Ptak Science Books    Rapid Post

Thinking about the “evolution” of music, I came to the 1940's and 1950's , and then to Jackson Pollock, and then to thinking about how his artwork evolved, and then, about how it might have truly evolved in a classic sense, like an evolutionary period.  None of this made much sense to me until I started thinking about the representation of Pollock fractally–and then things started to get interesting.  Could this work come about, again, as a result of the evolution of fractals?

Obviously the Pollock drips aren’t self-same, not easily observably, anyway–but what about statistically, especially under magnification?  

It turns out that someone has taken a look at this: Richard P. Taylor, et al, in “The Construction of Jackson Pollock’s Fractal Drip Paintings”¹This team concludes that–after analyzing paintings and films of Pollock painting them–“the painting process that...Pollock used a remarkably systematic method capable of generating intricate patterns that exhibit fractal scaling criteria”.  

I've never been comfortable with mid-century modern, but I must say that this Ollock/fractal business is interesting to think about, though I'm not sure it has anything to do with art. 

Notes:
1. Found in: Johnson, Colin G. Romero Cardalda, Juan Jesus.  “Introduction: Genetic Algorithms in Visual Art and Music–a Supplement”,  Leonardo, Volume 35, Number 2, April 2002, pp. 175-184 (Article)

Here’s another interesting book: The Art of Artificial Evolution: A Handbook on Evolutionary Art and Music by Juan Romero and Penousal Machado (Editors)bSpringer - Natural Computing Series Hardcover: 458 pag

The introduction to the Johnson ‘02 Leonardo article: “Leonardo has a long tradition of publishing work at the mutual frontier of art and science. We are pleased to present in the pages of Leonardo a special project that

History of Children, 1/7--the First Illustrated Rendering of the World for Kids: Occupations

JF Ptak Science Books  Post 1285

This is the first of seven installments on introducing 17th and 18th century children to wide ideas.  The text and images all come from the 1726 English translation of John Comenius' Orbita Pictus, and cover the following territory: Part 1, Occupations; Part 2, Anatomy; Part 3, Books and Book Arts; Part 4, the Sciences; Part 5, Morals and Philosophy; Part 6, Games and the Arts; and Part 7, the Military.  

"O Babees yonge, my Book only is made for youre lernynge” says what well may be the first book made in the West for children, written in the 14th century.  It was made for the eyes of noble blood, of course, and was basically a contribution towards how the children should act and behave, rather than teaching them anything outside of their immediate interactions with each other or their parents.  Books of manner and behavior was the dominant—if perhaps the only(?)—category of books for children until the late 16th century.

John Locke, in his Thoughts on Education (1691), suggests that "when a child begins to read, some easy, pleasant book, like Aesop's Fables or Reynard the Fox, with pictures if possible, should be put into his hands". He adds, "What other books there are in English of the kind above-mentioned, fit to engage the liking of children, and tempt them to read, I do not know, but am apt to think, that children, being generally delivered over to the method of schools, where the fear of the rod is to enforce, and not any pleasure of the employment to invite them to learn, this sort of useful books, amongst the number of silly ones that are of all sorts, yet have had the fate to be neglected; and nothing that I know has been considered of this kind out of the ordinary road of the hornbook, primer, Psalter, Testament, and Bible." (This quote from C.M. Watkins article in The Atlantic Monthly, 1880.)

Perhaps the most beautiful of early books for children is found behind this deeply designed title page, brought to us by Christoph Weigel (German, 1654-1726), the author, illustrator and engraver of Die Welt in einer Nuss oder die Historien vom Aufgang der Welt…¹ published in Nurnberg in 1726.  The book was a tall, thin production, with 16 pages of text and 43 engraved plates, much like this one, emblazoned with emblematic studies and dedicated to a particular point in the historical continuum.  And it was intended, believe it or not, for children—the title can be basically translated as “The World in a Nutshell” and was absolutely intended for kids, compressing all of the human story into 16 terse pages and a whole bunch of gorgeous illustration. This image shows the second millennium after the birth of Christ, illustrated with seven engravings (secula septem).

 

 But the first of all of the encyucloepdia-like books fasiohioned for children--and the first with illustratiions--belongs to the very well studied 13. The fteeple-crowned, 15. add te thefe The bald-pated, 14.

The Plow-man, i. yoketh Oxen, 3. to a Plough, 2. and holding the Flow-Rïlt, 4. in his left hand, and the Plow-ftaff, 5. in his right hand, ivith 'which he remcveth Clods, 6. he еutteth the Land {ivhich ivas manured afore ,uiifh Dung, 8.) with a Share, 7. and a Coulter, and makethFurrows, 9. Then he foweth the Seed, 10. and harroweth it in with a Harrow, 11. The Reaper, I2. jheareth the ripe Corn with a Sickle, 13. gatheteth up the handfuls, 14, und bindcth the Sheaves, 45.<t¿í Threiher, 16.; threfieth Corn en the Barn-floor, 17. ,with a Flail, 18. .*. toffeth it in a winnowing bafket, 19.andfo ivhen the Chaff', and the Straw, 20. are ßparatedfrom it, heputteth it into Sacks, 21 ,The Mower, 22. maketh Hay /я я Meadow, tutting do'wn Grafs with a Scythe, 23. and raketh it together üvith a Rake, 24. andmaketh up Cocks, 26. nvith a fork, 25. and carrieth it on Carriages, 27. into the Hay-barn, 28.

 

Vhe Bees find ota ¿r/warm, i. andfiet over it «Leader, 2. That Jkxiarm heing ready to fly away, is recalled hy the Tinkling ef a braaen Vefl.el, 3. and is put up into a neiv Hive, 4. They make little Cells nvith ßx comers, 5. and Jill them with Honey-dew, and make Combs, 6.cut of ivhich the Honey runneth, 7.The Partitions heing melted -with ßre, turn into Wax, 8.

Grinding

In a Mill, i. « ft'one, 2. runneth upen a ft one, 3.A Wheel, 4. turning them ahout, end grindeth Corn poured in by a Hopper, 5. endparteth the Bran, 6. falling into the .Tro ugh, 7. from the Mealßipping through aBolter, 8.Such a Mill voasßrft a Hand-mill, 9. then a Horfe-miil, 10.. then a Water-mill, 11. anda Ship-mill, i2. amdatlaßt a Wind-mill, 13.

 

History of Children, 7/7--the First Illustrated Rendering of the World for Kids: the Military

JF Ptak Science Books  Post 1291    Continuing the post 1285

"Taking the Scarecrows out of Wisdoms Gardens"

This is Part 7/7 of John Comenius' great work, the first illustrated instructional to children, first written in 1676 and then translated into English in 1726--it is from this translation that all of the images (below) are taken.  This is the second of seven installments on introducing 17th and 18th century children to wide ideas, the other sections including: Part 1, Occupations; Part 2, Anatomy; Part 3, Books and Book Arts; Part 4, the Sciences; Part 5, Morals and Philosophy; Part 6, Games and the Arts; and Part 7, the Military.  

The work itself: John Amos Comenius' Orbis Senfualium Piélus: Omnium Principalium in Mundo Rerun/ &f m Vita АШопит,  translated as Pictura et Nomenclatur, the Visible World, or A Nomenclature, and Pictures of all Chief Things that are int he World, translated into English by Charles Hoof...1726.

The purpose of the book, writes the translator in the introduction of the 1726 12th edition, is:  

To entice witty children to it, that they may not conceit a torment to be in the school, but dainty/are., For it is apparent, that children (even from their infancy almost) are delighted with Pictures, and willingly please their eyes with these fights: And it will be very well worth the pains to have once brought it to pafs, that fcare-crows may be taken away out of Wifdom's Gardens..."

Even at this early stage of publishing books for children it was easily recognized that children learn better when eased into their subject with pictures.  This is not so far off the mark with the moderns, and in its own way a precursor to the Dick and Jane and Dr. Seuss books--not so much for subject matter, but for the very act of putting a book into the hands of a child and getting them comfortable wit the idea of reading.  It seems to me that this is by far the most important lesson-the actual content at tis point is secondary to the act of holding a book.  

 

 

When aDeíign is undertaken, the Camp, i. is pitched, and the Tents if Canvas, гor Straw, Jarefaßened •with Stakes; and they entrench them aient, fer ßcurity's fake, •with Bulwark?, 4. and Ditches, 5. Sentinels, 6. ere alí'ofel; and Scouts, 7. arefent out.SaUyings-out, 8.ere made for Forage and Plunder-fake,where they often cope with the Enemy, 9. infiirmijhing.. The Pavilion of the Lord General is in the midßoftht Camp, 10.

il to hi fought, the Army is/et in order, and divided into the Front, 1.the Rear, 2.and the Wings, 3.The Foot, 4. mre intermixed •with the Horfe, 5,That is divided into Companies, this into Troops.Thefe carry Banners, 6. tho/e Flags, 7. in the midft of them.Their Officers are, Corporali, Enfigns, Lieutenants, Captains, 8. Commanders of the Horfe,9, Lieutenant Colonels, Colonels, and he that is the chief of all, the General. The Drummers, 10. and the Drumílades, 11. as alfo the Trumpeters, 12. call to Arms, and inßame the Soldier, At theßrß Onfet the Mofitets, 13. and Ordnance, 14. areßot off. After•wards thtyfight, 15. hand to hand •with Pikes and Swords. They that overcome are flain, 16. tr taken Prifoners, ,r run away, 17. They that are for the referve, 18. come upon thtm

A Sea-fight « terrihle, ,when huge Ships, like Caftles, run one upon another ivith their Beaks, 1 , or ßiatter one another with their Ordnance, 2. und/o, heing hored through, they drink in their own Deßnition, and art funk, 3. Or when they arefet on ßre, mid either hy the ßring of G un-powder, 4.

sr hreaking them doivn with Battering-engine!, 3, er demolifiing themwith great Guns, 4.or breaking through the Gates with a Petard, 5. er caßing Granadoes, 6. tut of M01 tar-pieces, 7. tuto the City,hy Engineers, 8. (ivho He hehind Leaguer-ha&ets, 9.) er 0 uerthroivingit avith Mines hy Pioneers, to. They thait are hefieged defend thtmfelves from the Walls, 11. •with ßre and ßones, &C or hreak out hy force, iz. A City that is taken hy Horra is plundered, deßroyed, andfomelimes laid evtl •with the ground.

 

History of Children, 6/7--the First Illustrated Rendering of the World for Kids: Games and the Arts

JF Ptak Science Books  Post 1290    Continuing the post 1285

"Taking the Scarecrows out of Wisdoms Gardens"

This is Part 6/7 of John Comenius' great work, the first illustrated instructional to children, first written in 1676 and then translated into English in 1726--it is from this translation that all of the images (below) are taken.  This is the second of seven installments on introducing 17th and 18th century children to wide ideas, the other sections including: Part 1, Occupations; Part 2, Anatomy; Part 3, Books and Book Arts; Part 4, the Sciences; Part 5, Morals and Philosophy; Part 6, Games and the Arts; and Part 7, the Military.  

The work itself: John Amos Comenius' Orbis Senfualium Piélus: Omnium Principalium in Mundo Rerun/ &f m Vita АШопит,  translated as Pictura et Nomenclatur, the Visible World, or A Nomenclature, and Pictures of all Chief Things that are int he World, translated into English by Charles Hoof...1726.

The purpose of the book, writes the translator in the introduction of the 1726 12th edition, is:  

To entice witty children to it, that they may not conceit a torment to be in the school, but dainty/are., For it is apparent, that children (even from their infancy almost) are delighted with Pictures, and willingly please their eyes with these fights: And it will be very well worth the pains to have once brought it to pafs, that fcare-crows may be taken away out of Wifdom's Gardens..."

Even at this early stage of publishing books for children it was easily recognized that children learn better when eased into their subject with pictures.  This is not so far off the mark with the moderns, and in its own way a precursor to the Dick and Jane and Dr. Seuss books--not so much for subject matter, but for the very act of putting a book into the hands of a child and getting them comfortable wit the idea of reading.  It seems to me that this is by far the most important lesson-the actual content at tis point is secondary to the act of holding a book.  

In a Play-houie, i. fivhich is trimmed ivith Hangings, 2. andcoveredivith Curtains,3.) Comedies and Tragedies are ailed, ivherein memorable things ere reprejented; as here, the Hißory of the Prodigal Sun, 4. and his Father, 5. hy килnm he is en/ertaiu'd, heing return d home. The Players kß heing in difguife; the Fool, 6. makith Jtßs.

 

 

The History of Children, 4/7--the Sciences and Learning /"Infinite Islands float in the Seas"

JF Ptak Science Books  Post 1287    Continuing the post 1285

"Taking the Scarecrows out of Wisdoms Gardens"

This is Part 4/7 of John Comenius' great work, the first illustrated instructional to children, first written in 1676 and then translated into English in 1726--it is from this translation that all of the images (below) are taken.  This is the second of seven installments on introducing 17th and 18th century children to wide ideas, the other sections including: Part 1, Occupations; Part 2, Anatomy; Part 3, Books and Book Arts; Part 4, the Sciences; Part 5, Morals and Philosophy; Part 6, Games and the Arts; and Part 7, the Military.  

The work itself: John Amos Comenius' Orbis Senfualium Piélus: Omnium Principalium in Mundo Rerun/ &f m Vita АШопит,  translated as Pictura et Nomenclatur, the Visible World, or A Nomenclature, and Pictures of all Chief Things that are int he World, translated into English by Charles Hoof...1726.

The purpose of the book, writes the translator in the introduction of the 1726 12th edition, is:  

To entice witty children to it, that they may not conceit a torment to be in the school, but dainty/are., For it is apparent, that children (even from their infancy almost) are delighted with Pictures, and willingly please their eyes with these fights: And it will be very well worth the pains to have once brought it to pafs, that fcare-crows may be taken away out of Wisdom's Gardens..."

Even at this early stage of publishing books for children it was easily recognized that children learn better when eased into their subject with pictures.  This is not so far off the mark with the moderns, and in its own way a precursor to the Dick and Jane and Dr. Seuss books--not so much for subject matter, but for the very act of putting a book into the hands of a child and getting them comfortable wit the idea of reading.  It seems to me that this is by far the most important lesson-the actual content at tis point is secondary to the act of holding a book.  

 

into the ßadotv oftheEatih,». it is darkened, nvhich ive tall an Eclipfe, or defeil.

But when the Moon runutth hetwixt the Sua and the Earth, 3. it covtilth it -with it 1 Jbaàomi; and this toe call the Eelipfe of the Sun, hecaufc it takethfrom us the ßght of the Sun, and its light;

neither doth the Sun/br all that fuffer any thing, eut the Earth.

is 360 degrees', ("•whereof every one maketh 60 Engliih Miles) or 2 1600 Miles, and yet it is tut a prick, compared •with the World, •whereof it is the Centre. - 4"hey mea/иrе the Longitude «fit hy Climates, 1. and the Latitude hy Parallels, *•

The Ocean, 3. cempajjeth it ahout, and ßve Seas voafi it, the Mediterranean Sea, 4. the Baltick Sea, 5. the Red Sea, 6. the Perfian Sea, 7, end the Calpian Sea, 8.

ей graduu»k CCCLX. (quorum quifque facit LX. Milliaria Anglica) vel 21600 Milliarium, & tamen eft puncbm, collata cum orhe, cujusCentrum eft. - Longitudinem ejus dimetiuntur Climatihus, 1. l-atitudinem, lineis Parallelis, 2.

Occanus, 3. amhit earn Se Maria V. perfundunt, Mtditerraneum, 4. Balticum, 5. Erythraum, t Perßcum, 7. ... _ Caffium, 8.

art uninhahitahle }.

the II. Temperate ones, 10. .10.

end the Torrid one, 11.

hahitable»

Beßdes it is divided into three Continents; thh of ours, 12. 'which isfubdividedinto Europe, 13. Afia, 14. Africa, 15. America, 16. ... 16. fivhofe Inhahitants are Antipodes to us) and the South Land, 17.. .1 7. yet unkno•wn.

They that d•well under the North Pole, 18. have the days and n'gbts 6 months long.

Inßnite Iflands float in tht Seas.

The Afp, 4. in the ßelds. The Boa ^rMild fnake)5.in Houfes. The Slow-worm, 6.

is hlind.

The Li2ard, 7. mid the Salamander, 8^ (that liveth long in ßre) have fee(.

The Dragon, 9. 2 winged Serpent, killeth ivith his Breath,

The Bafiliik, 10. with his Eyes;

And the Scorpion, 11. ,ivith his poi/onous tail.

fhe Earth-worm, i. the Earth.

The Caterpillar, 2. the Plant.

The Grafs-hopper, 3. the Fruit:.

The Mite, 4. the Gern.

The Timher-worm, 5. IVood.

The Moth, 6. a garment.

Tbe Book-worm, 7. я Book.

Maggots, 8. FUß and Cheefe.

Hand-worms, the Hair.

Thefiipping Flea, 9. the Loufe, 10. ostd the ßinking Wall-loufe, (Bug) 11. hite us.

The Tick, 12. it a Bkod-fucker.

The Siik-worm, 131 makethßlk.

The Pifmiie, 14. is painful.

SVSpider, ijy •wearveth a Cob•weh, nets for ßies.

The Snail, 16. tarrietjf about her Snail-horn.

. Lumbricns, 1. Terra m.

TL rue a, 2. Plantara.

Cicada, 3. Fruges.

Curculh, 4. Frumento»

Teredo (coffis) 5. Ligna.

Tinea, 6. vefiem,

Blatta, 7. _

Lihrum.

Tir mites, 8. Camem & Cafeum.

Acari, Capillum,

Saltans Pпlex, 9. Pediculus, 10. foutens Cimex, 11. mordent поз, 'Ricinus, п. fantruifugus eft.

Bombyx, 13. facit fericum.

Formica, 14. eft lahoriofa. ч Aranea, 1J. texit Araneum, retia inufcis. .

Cochlea, \6. Icircumfert Teftarbi

The e¿/e/rKingdoms qf In Europa noftrâ

Europe, are I funt Rtgna primaria, Spain,Spain, i. France, 2. Italy, 3. England, 4. Scotland, 5, Ireland, 6. Germany, 7; Bohemia, 8. Hungary, 9. Croatia, 10. Dacia, 11. Sclavonja, 12. Greece, 13. Thrace, 14. Podolia, 15. Tartary, 16. Lithuania, 17. Poland, 18. The Netherlands, 19. Denmark, 20. Norway, 21. Swedeland, 22. Lapland, 23. Finland, 24. Lifland, ?ç, Pruffia, 26. Mufcovy, 27, W Raffia, 28. .

 

The History of Children, 3/7: Books, Book-Making and Booksellers

JF Ptak Science Books  Post 1287    Continuing the post 1285

"Taking the Scarecrows out of Wisdoms Gardens"

This is Part 3/7 of John Comenius' great work, the first illustrated instructional to children, first written in 1676 and then translated into English in 1726--it is from this translation that all of the images (below) are taken.  This is the second of seven installments on introducing 17th and 18th century children to wide ideas, the other sections including: Part 1, Occupations; Part 2, Anatomy; Part 3, Books and Book Arts; Part 4, the Sciences; Part 5, Morals and Philosophy; Part 6, Games and the Arts; and Part 7, the Military.  

The work itself: John Amos Comenius' Orbis Senfualium Piélus: Omnium Principalium in Mundo Rerun/ &f m Vita АШопит,  translated as Pictura et Nomenclatur, the Visible World, or A Nomenclature, and Pictures of all Chief Things that are int he World, translated into English by Charles Hoof...1726.

The purpose of the book, writes the translator in the introduction of the 1726 12th edition, is:  

To entice witty children to it, that they may not conceit a torment to be in the school, but dainty/are., For it is apparent, that children (even from their infancy almost) are delighted with Pictures, and willingly please their eyes with these fights: And it will be very well worth the pains to have once brought it to pafs, that fcare-crows may be taken away out of Wifdom's Gardens..."

Even at this early stage of publishing books for children it was easily recognized that children learn better when eased into their subject with pictures.  This is not so far off the mark with the moderns, and in its own way a precursor to the Dick and Jane and Dr. Seuss books--not so much for subject matter, but for the very act of putting a book into the hands of a child and getting them comfortable wit the idea of reading.  It seems to me that this is by far the most important lesson-the actual content at tis point is secondary to the act of holding a book.  

 

The Ancients nvrit /яTables done over with wax ivith a hrazen Poitrel, i. ivith theJharp end, i. ivhereofletters ivereengraven, and ruhhed out again with the hread end, 3.

Afterwards they writ Letters with a fmall Reed, 4.

We ufe a Goofe-quill, 5. the Stem, 6. of which tue mabe with a Pen-knife, i7. then 'wt dip the Neb in an Ink-horn, 8. which is ßopped wit h aStopple, 9. andiiie put our Pens into /rPennar, 10.

 

makttjfik a Paper-mill, 4. of Linen nigs, 5. fiampedto Malh, 6. 'which heing taken up in Frames, 7. . he fpreadetb into Sheets, 8. andfetteth them in the Air that they may he dried.

1 vsenty -ßve cf thefe make a C¿iure, д. t•wenty Squirts a Ream, 10. and ten of thefe a Bale of Paper, 11.

That iwhich is to laß long is written on Parchment, 12

taketh them out one hy owe,and according to the Copy,(•which he hath faßened hefore him in a Viforum, 2.)compofeth •words in a Compoíing-ftick, 3. tilla Line he made; he putteth thefe in a Gaily, 4. till a Page, 6. he made, and thofe again in a Form, 7. and he locket h them up ., •. in Iron Chafes, 8. •with Quoins, 9. leß they Jhould drop out, and putteth them underthe Prefs, 10. Then the Prefs-man heateth it ever •with Printers Ink, hy means of Balls, 11. fpreadeth upon it the Papers put in the trinket, 12. •which heing put under the Spindle, 14. on the Coffin, 13. and prejfed down -with a Bar, 15. he maieth to taie mprejjton.

 

In times paß they g hued Paper to Paper, and rolled them up together, into one Roll, 1.

At this day the Book-hinder bindeth Rooks, ivhilß he ivipeth, 2. ever Papersßcrpt in Gum-water, and then foldeth them together, 3.

hec.teth ivith a hammer, 4.. J hen ßitcheth them up, ç. prefj'eth them ii a Prefs, 6. .ivhich hath tivo Screws, 7. glueth them on the hack, cutteth off the edges ivith a round Knife, 8. and at laß comer et b them ivith Parchment o/Leather, 9 maketh them handßme, andfetteth on Clefps, 10.

Olim agglutinahant Chartam Chartae,. convolvetiantque eas in unum Volumen, 1.

Hodiè Compaclor compingit Lihros, dum tergit, 2. Chartas niaceratas aqua glut tnef я, deinde complicat, 3. rr.alleav, 4.tum confuit, 5. cemprimitPrtlo, 6. quod hahet duos Cochlea!, ~. conglutinat dorio, demr.rginat rotundo Cuttro, 8. tandem veftit Membrana, vel Corio, д. efTormat, Scafiigit Unchndcs, 10.

A Book

A Book, as to its outtuard Shape, is either in Folio, i. er in Quarto, i, in Oitavo, 3. in Duodecimo, 4. either made to open Side-ways, ç er Long-ways, 6. ivith Bra2en Clafps, 7. or Strings, 8. and Square-boflês, 9.

Within are Leaves, 10. nvithfwo Pages, fometimes divided ivith Columns, 11. and Marginal Notes, 12t.

7 he Study, 1. ii a place -where a Student, 2 apart ftоm Men, fttteth alene, addicted to his Studies, 'whilji he readelh Booki, 3. luhith heing within hit reach be laytth open upon a Deflc, 4 andpickttb all theheß things out of them into hit ozvii Manual, 5.  cr market h them in than  with a Daih, 6. cr a little Star, 7. m the Margin.

 

History of Children, 2/7--the First Illustrated Rendering of the World for Kids: Anatomy

JF Ptak Science Books  Post 1286    Continuing the post 1285

"Taking the Scarecrows out of Wisdoms Gardens"

This is Part 2/7 of John Comenius' great work, the first illustrated instructional to children, first written in 1676 and then translated into English in 1726--it is from this translation that all of the images (below) are taken.  This is the second of seven installments on introducing 17th and 18th century children to wide ideas, the other sections including: Part 1, Occupations; Part 2, Anatomy; Part 3, Books and Book Arts; Part 4, the Sciences; Part 5, Morals and Philosophy; Part 6, Games and the Arts; and Part 7, the Military.  

The work itself: John Amos Comenius' Orbis Senfualium Piélus: Omnium Principalium in Mundo Rerun/ &f m Vita АШопит,  translated as Pictura et Nomenclatur, the Visible World, or A Nomenclature, and Pictures of all Chief Things that are int he World, translated into English by Charles Hoof...1726.

The purpose of the book, writes the translator in the introduction of the 1726 12th edition, is:  

To entice witty children to it, that they may not conceit a torment to be in the school, but dainty/are., For it is apparent, that children (even from their infancy almost) are delighted with Pictures, and willingly please their eyes with these fights: And it will be very well worth the pains to have once brought it to pafs, that fcare-crows may be taken away out of Wifdom's Gardens..."

Even at this early stage of publishing books for children it was easily recognized that children learn better when eased into their subject with pictures.  This is not so far off the mark with the moderns, and in its own way a precursor to the Dick and Jane and Dr. Seuss books--not so much for subject matter, but for the very act of putting a book into the hands of a child and getting them comfortable wit the idea of reading.  It seems to me that this is by far the most important lesson-the actual content at tis point is secondary to the act of holding a book.  

Septan Mtaies Hominis. A Man is ßrjt un Infant, 1. j Homo di primum Infasts, 1.

tien

a Tongue and Palate,
and Teeth, 16.
in the Cheek-hone.

A Man s Chin
is covered ivith a Beard, 14.
mnd the Eye
{in •which is the White
and the Apple)
•with Eye-lids,
and an Eye-hrow, 15.

The Hand heing clofed, is a Fift, 17. heing of en ira palm, i8, in the midß is the hollow, 19. of the Hand i the extremity is the Thumh, 10.iviehfour Fingers, the Fore-finger, 2s. the Middle-finger, гs. the Ring-finger, 23 and the Little-finger, 24. .

In every one are three ]o\ms, a. h. C. and asman knuckles, d. e. f. ivith a nail, 25.

In the Body are the Skin .nvith the Membranes, the Fleih ivith the Mafcles, the Chanel;, .,

the Griffles,
tie Bones andthe Boweli.

The Skin, i: heing puttV ef, the Fleih, 2. appeareth, vol in a continued lump, Lut heing diftnhuled, es it 'were in ßufi puddings, fuihuh they callMukks, ivhireof1here aie reckoned four hundred and five, heing the Chañeis cf the Spirits to move the Members.

The Bowels are the inward Members:

As in the Head,th.rBrains, 3. heing compajfed «bw with a Skull, and

In Corpore funt Cutis cum Mimhranis, Caro cum Mufcults, ..'

Canales,
Cartilagines,
Oßi & Vecera.

Cute, 1. detraíla,
Ca"o, 2. appaiet,
non continua raafsâ,
fed dil.tributa,
tanquam in farcimina,
quos vocant Mu/tules,
quorum numerantur
quadringenti quinque,
canales Spirituum,
ad movendum Memhra,

Vijcera funt Memhra interna:

Ut in Capite, Cerehrum, 3. cire umda tum Crem», Sc

The Arteries currying Blood from the Heart; 4'he Veins returning the Mood to the Heart} The Nerves carrying Setife and Motion throughout the Body from the Brain. You jkallßnd thefe three, 1. t'very inhere joined together. Beßdes, from the Mouth into the Stomach it the Gullet, 2, the way of the meat and drini, and-hy it to the Light!, the Wezand, 5. for hr.athing; f cm the Stomach to the Arfe it a great Gut, 3. to purge out the Ordure; from the Li-ver to the Bladder, the Ureter, 4. for making 'wJter. . Tie Bones are in the Head, the Skull, 6. the ttuo Cheek-bones, 7. with thirty tTvo Teeth, 8. Then the Back-bone, 9. the Pillar of the Body, tonfifling of thirty four turning Joints, that the Body may hend itfelf The Ribs, re. ,uihereof there are twenty four. The Breaft-bone, 11. the five Shoulder-blades, ii. the Buttock-bone, 13.. the bigger Bone in the . Atta, 15. *W/¿/kfi'crBone inthi Arm. V-Л ù •; vi; Mußcal Типа. The Nofe, 3. fcenteth fmelh and ßinhs. The Tongue, 4. •with the reef of the Mouth taßet Favours, •what is fweet or hitter, keen or hiting, four or каф. The Hand, 5. hy touching difcerneth the quantity and q: ality of things; the hot and cold, the moifl and dry, She hard andfft, the fnooth and rough, the bsavy and light. The in•ward Sen fes are three. . The Common Senfe, 7. under the forepart of the head, afprehendeth i t/.ings taken from the oufward Senfes. The Phantafye, 6. under the crown of the head, judgeth ofthefe things, t hinket h and drcameth The Memory, 8. under the hinder part of the head, layeth up every thing end fctcbeth them out; it Ufethfome, and this is forgetfulnefs. Sleep, is the reft of the Senfes. The Soul is the Life tf the Body, oie in the ivhole. Only Vegetative in Plants; Withal Seníltive in Animals; And alfo Rational in Men. This confifteth in three things; In the Underftanding, wherehy it judget h, and underßandethy - a thing good and evil, or true, or apparent. In the Will, •whereby it choofeth, and deßreth, tr rejeéleth, er mißiketh a thing knovn. In the Mind, •whereby it purfueth Anima eft vita corpoiii, una in tota. Tantum Vegetativa In Plantis; Simul Senßtinsa in Ahímalibus J, Etiam Rational is in Hernie/i liaec coniiftet in trihu»; In Mente (Intelleflu) qua cognofcit, & intelligit, honum ac malum, vel verum, vel apparent» In Voluntate-, qua eligir, Sc concupifcit, aut rejicit, & averfatur cogniuim. In Animo, quo prpfequituv