JF Ptak Science Books Quick Post
![]()
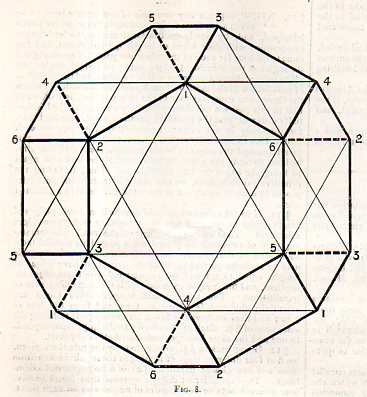
The question above is probably seldom asked and probably even less than so required, but it sure does look good for the title of a post. The pillowed polyhedra came into light while I was breezing through some issues of the British Nature magazine for 1893/4--the title of the work of course was a lovely thought and the author of the paper was the mega-gifted and highly significant Lord Kelvin (William Thomson), but the bait that made me swallow the hook on the paper was the illustration.
There are many (i.e., 1,496,225,352) different forms of the convex 14-faced polyhedron tetrakaidekahedron (see Wolfram Math for a quick summary)--this is the first I can remember being displayed on a 19th century pillow. Kelvin was particularly interested in displaying geometrical figures in three dimensional space, and would return to the issue numerous times, particularly in the Baltimore Lectures on Molecular Dynamics and the Wave Theory of Light (see page 606ff).

Notes:
Lord Kelvin, (William Thomson, 1824-1907), "On the Homogeneous Division of Space", in Nature, two issues, as follows: (1) 8 March 1894, pp 445-448; and (2) 15 March 1894, pp 469-471. A version of this paper appears slightly earlier (17 January) in the Proceedings of the Royal Society.
Both papers are available for purchase via our blog bookstore, here.
These are remarkably interesting papers--especially considering their brevity.
It is interesting to note the list of what Thomson "is known for" in his Wiki entry:
- Joule–Thomson effect
- Thomson effect (thermoelectric)
- Mirror galvanometer
- Siphon recorder
- Kelvin material
- Kelvin water dropper
- Kelvin wave
- Kelvin–Helmholtz instability
- Kelvin–Helmholtz mechanism
- Kelvin–Helmholtz luminosity
- Kelvin transform
- Absolute Zero
- Kelvin's circulation theorem
- Stokes' Theorem
- Kelvin bridge
- Kelvin sensing
- Kelvin equation
- Kelvin-Varley divider
- Magnetoresistance
- Coining the term 'kinetic energy'




Comments