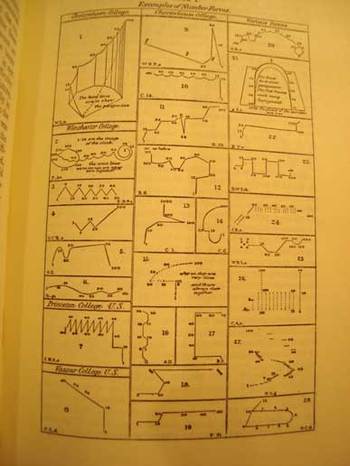
I wanted to return and add a bit to an earlier notice concerning a series of drawings that I found utterly fascinating—the earliest illustrations of the active formation representing visualized human thought. (I know that this titling is ungainly, but it seems to be the least inelegant solutions to stating the idea of what the images represent.) It so happens that Francis Galton approached this same issue—though without pictorial representation—in an earlier paper with the unusual and provocative title of “Visions in Sane Persons” (1881). Working further through this thesis and publishing an illustrated report in 1882, he continued, and greatly expanded, the study in a 26-page chapter called “Number-Forms” in his book Inquiries into Human Faculties and its Development (1883, with a second edition appearing in 1909). Galton includes another 71 images of visualizing arithmetic, plus others on general images of mental images of numbers and letters—there is also a small but beautiful section on associations between colors and numbers and letters. (These are all depicted in the first four images on this page.)
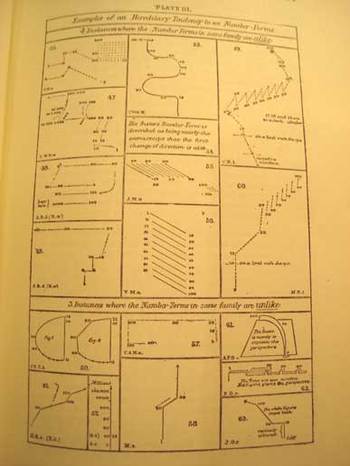
G.T.W. Patrick (a professor of philosophy at the state university of Iowa) published one of the earliest papers in response to Galton’s work. In “Number-forms”, published in the Popular Science Monthly in February 1893 (pp 504-515, and “illustrated”), Patrick addresses and expands Galton’s work somewhat, including another eighteen wonderful illustrations of similar images.
But the path back to Galton is not quite a straight one. Galton was initially concerned with imaging of numbers and numbers forms while people were performing mental calculations. Patrick on the other hand asked his subjects if they had associative images in their mind of numbers—formally, he asked them if the number series of 1-9 presented itself in a visual, representative way in their minds. In the second and third parts of his three-part inquiry, he asked the same question about letters and the alphabet, and then, thirdly, if they perceived any sense of color from letters and numbers, and what then what those exact relationships were.

It is interesting that in the studies of Galton and Patrick that over time in each of the subjects tested that (in Galton’s words) the images were “absolutely unchangeable except for a gradual development of complexity”. Since I (like Galton, which is probably the only time I will ever be able to associate myself with this man
in terms of familiar traits) have no such images in my head when I think about mathematics or numbers or letter or words in general, it is remarkable to me on the human scale that people who have these associations would have the same ones time after time. A movable feast, as it were. Of course it would make sense that this reference system would be constant—but for someone that doesn’t ‘see” these images at all, the fact that they are so flowing and lucid and unchanging is simply difficult for me to imagine. (In a few weeks I'll return to this issue, looking at how some prodigiously gifted people "see" with their special attributes.)
Images below are from the Patrick paper:


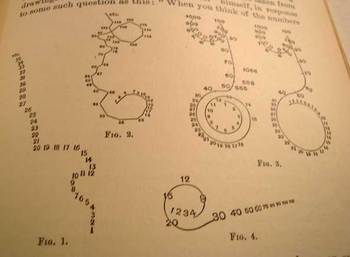
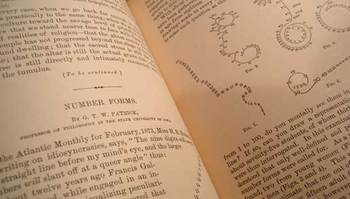
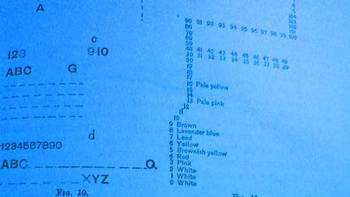

Comments